Conclusie van het "twee pieken experiment"

[wnvl1]

Waarom vertoont het licht twee maxima bij afbuiging door de zon?

Cfr. https://www.mathpages.com/rr/s8-09/8-09.htm



Alles vertrekt van de Schwarzschildmetriek

\(c^2d\tau^2 = \bigg(1-\frac{r_s}{r}\bigg)dt^2-\frac{dr^2}{1-r_s/r}-r^2(d\theta^2+\sin^2 \theta d\phi^2)\)


Welke benaderingen maakt Einstein?

1. Heel wat benadering zijn te herleiden tot

\(\sqrt{1 - \frac{2M}{r}} \approx 1 - \frac{M}{r}\)

met \(M\) de massa van de zon.
Dit genre van benadering wordt meermaals toegepast. Kwadratische en hogere machten van \(\frac{M}{r}\) worden verwaarloosd.

2. Het licht beweegt op een kromme baan rond de aarde. Einstein maakt hier in een DEEL van zijn redenering een rechte van. Niet voor de volledige redenering.

3. Einstein maakt gebruik van het principe van Huyghens. In een gekromde ruimte is het principe van Huyghens niet zomaar van toepassing. Huyghens is gebasserd op het zoeken van omhullende aan cirkels. Die cirkels gaan in een gekromde ruimte ellipsen worden, Ik heb nergens teruggevonden hoe je het principe kan aanpassen, wel is zeker dat het niet van toepassing is op de manier waarop Einstein het gedaan heeft.

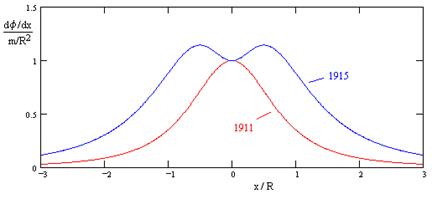
Hoe kan je de 2 pieken verklaren?

De lichtsnelheid (gemeten in het assenstelstel van een verre waarnemer b.v. op de aarde) verandert sterker in de radiale richting dan in de richting looodrecht daarop.

In radiale richting PA heb je distorsie in tijd en ruimte.
\(c_{rad} = 1 - \frac{2M}{r}\)

In richting PB alleen distorsie in ruimte.
\(c_{\perp rad} = \sqrt{1 - \frac{2M}{r}} \approx 1 - \frac{M}{r}\)


Er zijn nu twee effecten die spelen als we de baan bestuderen. Ikj leg beide effecten intuïtief uit.

1. Hoe groter \(\theta\), hoe groter \(r\) (i.e. hoe verder van de zon), hoe kleiner de verandering in \(c\). Dit geldt zowel voor de radiale als de loodrechte component. Gevolg is een kleinere rotatie, bij groter \(\theta\).
2. Hoe groter \(\theta\) (i.e. hoe verder van de zon), hoe groter de component loodrecht op de radiale snelheid doorweegt. Deze component is sterker geïmpacteerd door de kromming dan de radiale component. Gevolg is een grotere rotatie, bij grotere \(\theta\).

Beide effecten zijn tegengesteld, dus er zijn twee pieken.

[wnvl1]

Ik heb ook nog naar de Jupyter notebook van OOOVincentOOO gekeken.

Dit doet vermoeden dat de 2 pieken niet altijd voorkomen. Mijn uitleg hierboven kan het voorkomen van 2 pieken verklaren.

Het kan echter ook zijn dat effect (2) uit mijn vorige post onderaan, te zwak is om effect (1) te compenseren. Dan zou je maar één piek hebben. Mijn laatste zin "Beide effecten zijn tegengesteld, dus er zijn twee pieken." is achteraf gezien te sterk geformuleerd. Maar dat kan je niet intuitief aanvoelen, lijkt mij. Dat moet uit de berekening of simulatie zoals OOOVincentOOO gedaan heeft volgen, denk ik.

[Professor Puntje]

Dank voor je commentaar! Mag ik daaruit concluderen dat volgens jou ook bij een exacte berekening (dus zonder de op MathPages gebruikte benaderingen) in een xy-frame er voor een lichtstraal die de zon rakelings passeert mogelijkerwijs twee pieken in de getoonde grafiek optreden? En dat een nadere berekening/simulatie moet uitwijzen of dat ook inderdaad het geval is.

[OOOVincentOOO]

Ik ben geen Natuurkundige met veel ervaring in GR. Maar ik ruim ervaring in analyses van meetgegevens etc. Echter als ik studeer vind ik: volgens de Schwarzshield geodesics op [Wiki] (hetzelfde startpunt als wnvl1):

Orbits of test particles:
1) The solution of the orbit equation is:

$$ \varphi =\int {\frac {dr}{\pm r^{2}{\sqrt {{\frac {1}{b^{2}}}-\left(1-{\frac {r_{\rm {s}}}{r}}\right)\left({\frac {1}{a^{2}}}+{\frac {1}{r^{2}}}\right)}}}}$$

Waarbij \(a\) en \(b\):

$$h={\frac {L}{\mu }}=r^{2}{\frac {d\varphi }{d\tau }} \\ a={\frac {h}{c}},\\b={\frac {cL}{E}}={\frac {hmc}{E}}$$

where L is the total angular momentum of the two bodies, and μ is the reduced mass. For the photonic case, we also need to specify a number corresponding to the ratio of the two constants, namely m h E, which may be zero or a non-zero real number.

2) Bending of light by gravity:
In the limit as the particle mass m goes to zero (or, equivalently if the light is heading directly toward the central mass, as the length-scale a goes to infinity), the equation for the orbit becomes:

$$\varphi =\int {\frac {dr}{r^{2}{\sqrt {{\frac {1}{b^{2}}}-\left(1-{\frac {r_{\rm {s}}}{r}}\right){\frac {1}{r^{2}}}}}}}$$

Expanding in powers of r s r, the leading order term gives angular deflection δφ for a massless particle coming in from infinity and going back out to infinity:

$$\delta \varphi \approx {\frac {2r_{\rm {s}}}{b}}={\frac {4GM}{c^{2}b}}$$

Intuitie wat deze vergelijking voorstelt:
Hier een grafiek van deze vergelijking. Ik krijg de exacte schaalverdeling nog niet goed. Eigenlijk dient \(\varphi=1.74"\). Echter men kan duidelijk zien hoe deze functie zich gedraagt. Hier is te zien dat de deflectiehoek convergeerd (linker grafiek). In de buurt van de zon krijg je een rare spiraal (grafiek recht in \(x\) en \(y\)). Deze spiraal volgt de vergelijking van \(\varphi\) nabij centrale massa van de zon.

Mijn begripsvorming.
Dus volgens Wiki staat dat de limiet de orbit/deflectie van een lichtstraal: gelijk is aan een massaloos particle en/of: licht dat direct naar de centrale massa gaat.

De simulatie van Lichtbuiging [Youtube] laat zien dat in de instabiele zone (in de buurt van centrale massa) twee pieken ontstaan. De hoekdeflectie verdeling verloopt van: Gaussisch naar Arcsin via een twee piek verdeling. Deze transitie gebeurt vanaf: \(r_{s}<2\) de instabiele zone nabij de centrale massa.

Dus voor mij is het niet verwonderlijk dat er twee pieken ontstaan.

De limiet om de deflektie te bepalen van een massaloos partikel is dus gelijk aan de limiet van een partikel dat naar de centrale massa gaat via instabiele zone.

[Professor Puntje]

Ten eerste heb je daar te maken met een benadering voor de totale afbuiging, die hier niet interessant is. Ten tweede vertoont licht dat zich direct naar de centrale massa van de zon beweegt helemaal geen afbuiging, immers waar zou dat licht dan naar moeten afbuigen?

[OOOVincentOOO]

Beste Professor,

Jouw commentaar is erg mager en niet duidelijk.

Ten eerste heb je daar te maken met een benadering voor de totale afbuiging,

Wat is daar? Welke benadering? Alles op Wiki is gebaseerd op precies dezelfde vergelijking als: wnvl1 verteld in opening post. [Wiki]

Ten tweede vertoont licht dat zich direct naar de centrale massa van de zon beweegt helemaal geen afbuiging, immers waar zou dat licht dan naar moeten afbuigen?

Hoe ik begrijp is de limiet nemen naar een massaloos deeltje hetzelfde als licht wat zicht beweegt naar de centrale massa. Dat is de \(1/a^2\) uit mijn vorige post.

Waarschijnlijk ben ik verkeerd maar ik heb het idee dat je bevooroordeeld mijn bijdrage bekijkt. Je geeft kritiek en stelt niet eens inhoudelijke vragen. Evenmin vragen of ik iets nader wil verklaren.

Voor eerlijk te zijn zou ik liever inhoudelijke kritiek en vragen krijgen van iemand met meer ervaring. Jij hebt immers pagina na pagina gepost zonder duidelijke gesloten verklaring. Daardoor vind ik jouw opinie niet onafhankelijk.

Het klopt mijn reactie is bot en kort. Indien je reageert met: ja maar dit of dat of: ik heb hier geen zin in zou ik erg laag vinden. Jij hebt ook liever geen commentaar van grafiek jongetje OOOVincentOOO.

[Professor Puntje]

Vriendelijk verzoek de discussie over je simulatie en de eventuele betekenis daarvan voor de twee pieken in het daaraan geweide topic voort te zetten. wnvl1 heeft inderdaad meer kennis en ervaring met de ART dan ik, en zal je wellicht wel verder kunnen helpen. Volgens mij zegt het gedrag van licht nabij de schwarzschildradius weinig of niets over de beweging van licht dat rakelings langs de zon scheert, dus ik kan daar verder dan ook niets mee. Maar wie ben ik? We zullen zien of het piekenprobleem deze keer wel opgelost gaat worden...

[wnvl1]

Dank voor je commentaar! Mag ik daaruit concluderen dat volgens jou ook bij een exacte berekening (dus zonder de op MathPages gebruikte benaderingen) in een xy-frame er voor een lichtstraal die de zon rakelings passeert mogelijkerwijs twee pieken in de getoonde grafiek optreden? En dat een nadere berekening/simulatie moet uitwijzen of dat ook inderdaad het geval is.

Ja, dat is mijn conclusie. Ik hoop dat mijn uitleg duidelijk maakt dat er een intuïtieve verklaring is voor de mogelijke 2 pieken. Maar uiteindelijk moet natuurlijk alles volgen uit de berekening.
Hoe groot de fout is veroorzaakt door de benaderingen is ook niet zomaar te zeggen lijkt mij. Het zijn veel kleine dingetjes die bij elkaar komen.

[Professor Puntje]

Mooi - dank!

[wnvl1]

Ik ben geen Natuurkundige met veel ervaring in GR. Maar ik ruim ervaring in analyses van meetgegevens etc.

Het lijkt mij dat omdat de metriek vastligt en Schwarzschild is, dit een wiskundig probleem is waar vanaf dan weinig ART bij komt kijken. Ik moet eerst de wiki pagina nog eens goed lezen.

[wnvl1]

Vriendelijk verzoek de discussie over je simulatie en de eventuele betekenis daarvan voor de twee pieken in het daaraan geweide topic voort te zetten. wnvl1 heeft inderdaad meer kennis en ervaring met de ART dan ik, en zal je wellicht wel verder kunnen helpen. Volgens mij zegt het gedrag van licht nabij de schwarzschildradius weinig of niets over de beweging van licht dat rakelings langs de zon scheert, dus ik kan daar verder dan ook niets mee. Maar wie ben ik? We zullen zien of het piekenprobleem deze keer wel opgelost gaat worden...

Maar op zich is de oplossing van OOOVincentOOO wel de exacte oplossing. Zonder de benaderingen van Einstein. Dus dat zou wel relevant moeten zijn. Of ben ik verkeerd?

[Professor Puntje]

Wat er gebeurd is dat is dat OOOVincentOOO en ik met hulp van anderen een simulatie in Python hebben gemaakt van de beweging van lichtdeeltjes die langs de zon schieten. Dat heeft na het nodige geploeter fraaie plaatjes opgeleverd. Zie daarvoor het topic: viewtopic.php?f=85&t=212427

Echter is OOOVincentOOO zich op zeker moment gaan focussen op wat er met licht gebeurt nabij de schwarzschildradius. Maar dat is niet het probleem waar ik hier in geïnteresseerd ben. Wat nabij de schwarzschildradius gebeurt zegt - voor zover ik kan zien - weinig of niets over het al dan niet optreden van twee pieken in het grafiekje van licht dat rakelings langs de zon scheert. OOOVincentOOO meent nu dat ik hem onrecht doe door aan zijn simulaties van het gedrag van licht nabij de schwarzschildradius niet meer aandacht te schenken. Misschien dat jij ziet hoe zulke simulaties relevant voor dit topic zijn, maar ik zie het niet. Een simulatie van licht dat rakelings langs de zon scheert is natuurlijk wel relevant. En zo'n simulatie hebben we toen ook al gevonden.

[OOOVincentOOO]

Volgens mij lees je mijn bijdragen niet. Je bent vooringenomen. Lees mijn eerste post in dit draadje eens goed en bestudeer.

Stel gewoon een vraag als ik onduidelijk ben. En niet vooringenomen conclusies trekken en kritiseren.

Ik lees litteratuur en maak observaties, experimenteer en maak simulaties en toets aan theorie/praktijk. Hieruit probeer conclusies te trekken.

Op deze manier maak je de theorie eigen.

Sorry PROFESSOR als ik niet wetenschappelijk bezig ben.

[wnvl1]

Hoe ik begrijp is de limiet nemen naar een massaloos deeltje hetzelfde als licht wat zicht beweegt naar de centrale massa. Dat is de \(1/a^2\) uit mijn vorige post.

Ik weet dat niet. Die zin is raar geformuleerd in het wikipedia artikel. Ik moet eens uitzoeken wat daar achterzit. Of als je zelf die formulering kan uitleggen...

In the limit as the particle mass m goes to zero (or, equivalently if the light is heading directly toward the central mass, as the length-scale a goes to infinity), the equation for the orbit becomes

Bedoelen ze dat de massa naar 0 gaat of dat r naar 0 gaat?
Er moet een uitgebreider artikel zijn waar dit beschreven wordt.

De link met die integraal moet ik ook nog beter begrijpen.

[wnvl1]

https://www.researchgate.net/publicatio ... s_approach

hoofdstuk 6 maakt het wel duidelijk.

Je moet met je integraal wel voldoende wegblijven van de 0. Anders heb je licht dat invalt op de zon en dat was niet direct de bedoeling. De r komt tot van oneindig, gaat tot zijn kortste afstand, ik zeg maar iets, tot 3 en dan terug naar + oneindig. Het zijn die pieken die jullie wilden bestuderen. Maar eigenlijk is dat wel wat OOOVincentOOO aangeeft in de uitleg. Dus ik denk dat OOOVincentOOO het wel doorheeft.