Een weerstand van 1,8 k en 0,25 Watt, kan bij een gelijkspanning van max 21 Volt, een tijdje overleven.
Deze weerstand moet bij aanvang bij 50 Volt, 1,4 Watt vermogen verwerken, pas bij 21 Volt komt deze
uit de gevaren zone...afhankelijk ook nog van de omgevingstemperatuur.
In de praktijk gaat dit op langere duur problemen geven, de weerstand gaat te vaak buiten zijn specs.
Dan zou je de specs. van de weerstand erbij moeten zoeken, wat voor dit type de max. toelaatbare
overbelasting en gedurende welke tijd en temperatuur.
Ik zou zo een risico voor 10 cent niet nemen en gewoon een weerstand nemen die 2 Watt aan kan.
- WillemB
- Artikelen: 0
- Berichten: 654
- Lid geworden op: do 20 feb 2014, 17:51
Re: maximaal vermogen
Sinds de uitvinding van tijd, hebben we het niet meer, en kunnen we het ook niet meer vinden.
En wie haast heeft moet langzamer lopen.
En wie haast heeft moet langzamer lopen.
- ukster
- Artikelen: 0
- Berichten: 4.917
- Lid geworden op: za 28 nov 2015, 10:42
Re: maximaal vermogen
Mee eens,dus bij lage frequenties (lange periodetijd) zitten we zeker in een gevarenzone.(>0,25W)
Er moet dus een minimale frequentie zijn waarbij we definitief uit de gevarenzone <0,25W) komen
Er moet dus een minimale frequentie zijn waarbij we definitief uit de gevarenzone <0,25W) komen
- WillemB
- Artikelen: 0
- Berichten: 654
- Lid geworden op: do 20 feb 2014, 17:51
Re: maximaal vermogen
De temperatuur gaat dan een rol spelen, wat is de max. temperatuur die de weerstand langere tijd aan kan.
Dan zou je dus meer baat hebben bij een temperatuur curve over langere tijd, of je de limiet niet overgaat.
Als voorbeeld, als je de weerstand opsluit in een gesloten doosje, dan zal het opwarmen tot een bepaalde temperatuur,
afhankelijk van de omgeving of er makkelijk afgekoeld kan worden.
Voorbeeld, waarom veel adapters tegenwoordig ontploffen, omdat de goedkope afvalk Elko maar 85 graden aan kan,
en de omgeving heter wordt dan 85 graden in zo een klein kastje. En dat komt niet eens door de Elko zelf.
Dan zou je dus meer baat hebben bij een temperatuur curve over langere tijd, of je de limiet niet overgaat.
Als voorbeeld, als je de weerstand opsluit in een gesloten doosje, dan zal het opwarmen tot een bepaalde temperatuur,
afhankelijk van de omgeving of er makkelijk afgekoeld kan worden.
Voorbeeld, waarom veel adapters tegenwoordig ontploffen, omdat de goedkope afvalk Elko maar 85 graden aan kan,
en de omgeving heter wordt dan 85 graden in zo een klein kastje. En dat komt niet eens door de Elko zelf.
Sinds de uitvinding van tijd, hebben we het niet meer, en kunnen we het ook niet meer vinden.
En wie haast heeft moet langzamer lopen.
En wie haast heeft moet langzamer lopen.
- ukster
- Artikelen: 0
- Berichten: 4.917
- Lid geworden op: za 28 nov 2015, 10:42
Re: maximaal vermogen
warmte- en stromingsleer lijkt mij een interessant vakgebied.
- Professor Puntje
- Artikelen: 0
- Berichten: 7.574
- Lid geworden op: vr 23 okt 2015, 23:02
Re: maximaal vermogen
Volgens mij is dit de integraal die we nodig hebben:
Bron: http://www.wolframalpha.com/input/?i=%5Cint_0%5E(3*%5Ctau)++(%5Cexp(-t%2F%5Ctau))%5E2+dt
Bron: http://www.wolframalpha.com/input/?i=%5Cint_0%5E(3*%5Ctau)++(%5Cexp(-t%2F%5Ctau))%5E2+dt
- ukster
- Artikelen: 0
- Berichten: 4.917
- Lid geworden op: za 28 nov 2015, 10:42
Re: maximaal vermogen
In deze uitdrukking staat de som van de kwadraten van de momentele waarden over een hele periode (integraal), maar ik mis hierin de topwaarde van 50V. dus dan zou er staan 2500 X1/2 tau (1-e^-6)
De effectieve waarde in het kwadraat is het gemiddelde van de som van de kwadraten van de momentele waarden over een hele periode, en hiermee is het langdurig gemiddelde vermogen in de weerstand te berekenen.
De effectieve waarde in het kwadraat is het gemiddelde van de som van de kwadraten van de momentele waarden over een hele periode, en hiermee is het langdurig gemiddelde vermogen in de weerstand te berekenen.
- WillemB
- Artikelen: 0
- Berichten: 654
- Lid geworden op: do 20 feb 2014, 17:51
Re: maximaal vermogen
Volgens mij hebben we het niet over effectieve waarde.
Zoals eerder opgemerkt, is het vermogen afhankelijk van het gemiddelde van het kwadraat van de spannings vorm,
en het is geen sinus spanning.
Zoals eerder opgemerkt, is het vermogen afhankelijk van het gemiddelde van het kwadraat van de spannings vorm,
en het is geen sinus spanning.
Sinds de uitvinding van tijd, hebben we het niet meer, en kunnen we het ook niet meer vinden.
En wie haast heeft moet langzamer lopen.
En wie haast heeft moet langzamer lopen.
- ukster
- Artikelen: 0
- Berichten: 4.917
- Lid geworden op: za 28 nov 2015, 10:42
Re: maximaal vermogen
Pgemiddeld is toch (Ueff)2 / R
- Professor Puntje
- Artikelen: 0
- Berichten: 7.574
- Lid geworden op: vr 23 okt 2015, 23:02
Re: maximaal vermogen
\( \mbox{P}_{gem} = \frac{1}{\mbox{T}} \, \int_0^T \mbox{P}(t) \, \mbox{d} t \)
\( \mbox{P}_{gem} = \frac{1}{\mbox{T}} \, \int_0^T \frac{(\mbox{U}(t))^2}{\mbox{R}} \, \mbox{d} t \)
\( \mbox{P}_{gem} = \frac{1}{\mbox{T} \mbox{R}} \, \int_0^T (\mbox{U}(t))^2 \, \mbox{d} t \)
\( \mbox{P}_{gem} = \frac{1}{3 \tau \mbox{R}} \, \int_0^{3 \tau} \left (\hat{\mbox{U}} e^{\frac{- t}{\tau}} \right )^2 \, \mbox{d} t \)
\( \mbox{P}_{gem} = \frac{\hat{\mbox{U}}^2}{3 \tau \mbox{R}} \, \int_0^{3 \tau} \left (e^{\frac{- t}{\tau}} \right )^2 \, \mbox{d} t \)
- WillemB
- Artikelen: 0
- Berichten: 654
- Lid geworden op: do 20 feb 2014, 17:51
Re: maximaal vermogen
@ Ukster, die formule is voor sinus vormige spanningen, maar jij laat in de grafiek een ontladings curve via een e macht zien.
gerelateerd hieraan, zoek maar eens op true RMS en crest factor, hoe ze daar vermogen berekenen.
gerelateerd hieraan, zoek maar eens op true RMS en crest factor, hoe ze daar vermogen berekenen.
Sinds de uitvinding van tijd, hebben we het niet meer, en kunnen we het ook niet meer vinden.
En wie haast heeft moet langzamer lopen.
En wie haast heeft moet langzamer lopen.
- ukster
- Artikelen: 0
- Berichten: 4.917
- Lid geworden op: za 28 nov 2015, 10:42
Re: maximaal vermogen
Ik ben het niet met je eens Willem B, deze expressie is toepasbaar op elke spanningsvorm
Pgem=2500/(3.tau.1800)x1/2.tau.(1-e^-6)Watt
Pgem=2500/(3.tau.1800)x1/2.tau.(1-e^-6)Watt
- Professor Puntje
- Artikelen: 0
- Berichten: 7.574
- Lid geworden op: vr 23 okt 2015, 23:02
Re: maximaal vermogen
Als het goed is moet tau er weer uit weg vallen.
- klazon
- Pluimdrager
- Artikelen: 0
- Berichten: 7.933
- Lid geworden op: ma 09 mei 2005, 23:52
Re: maximaal vermogen
Indirect gaat het natuurlijk wel over de effectieve waarde. Die is kort gezegd RMS, root-mean-square, oftewel het kwadraat van de spanningsvorm, daar het gemiddelde van en daar weer de wortel uit. Maar aangezien we voor de bepaling van het vermogen het kwadraat van de effectieve spanning nodig hebben kunnen we de wortelbehandeling laten vervallen.WillemB schreef: Volgens mij hebben we het niet over effectieve waarde.
Zoals eerder opgemerkt, is het vermogen afhankelijk van het gemiddelde van het kwadraat van de spannings vorm,
en het is geen sinus spanning.
En dat het geen sinus is doet niks ter zake, dit verhaal geldt voor elke periodieke vorm.
- WillemB
- Artikelen: 0
- Berichten: 654
- Lid geworden op: do 20 feb 2014, 17:51
Re: maximaal vermogen
@ Ukster, in de grafiek te zien heb je een ontlading van een condensator dan krijg je te maken met deze e macht formule,
voor de spannings vorm: :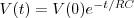
voor de spannings vorm: :
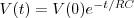
Sinds de uitvinding van tijd, hebben we het niet meer, en kunnen we het ook niet meer vinden.
En wie haast heeft moet langzamer lopen.
En wie haast heeft moet langzamer lopen.
- ukster
- Artikelen: 0
- Berichten: 4.917
- Lid geworden op: za 28 nov 2015, 10:42
Re: maximaal vermogen
@willemB, dat is helemaal correct ,waar waar doel je hiermee nu op?