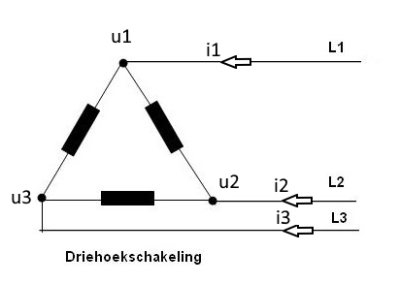
Ik werk verder met de tekening van xilvo.
Dus L1, L2 en L3 zijn de lijnen. Deze lopen van de energieleverancier naar de verbruiker. Op die lijnen lopen de lijnstromen i1, i2 en i3. De kant van de bron is niet meegetekend. Daar kunnen de bronnen in driehoek of in ster geschakeld zijn. Je kan altijd het ene omrekenen naar het andere. Als ze in ster staan, kan je het sterpunt doortrekken en dat is dan de neutrale lijn.
De spanning tussen de lijn L1 en de neutrale lijn is de fasespanning, die is hier u1.
De spanning tussen u1 en u2 is een lijnspanning. Je kan die dan u12 noemen.
De impedantie aan de verbruikerskant tussen lijn 1 en lijn 2 is Z12. De stroom door Z12 noem je dan best i12. Over Z12 staat de lijnspanning u12.
In dit geval is er geen neutrale lijn, dus de som van i1, i2 en i3 moet nul zijn. Complexe getallen zijn vectoren, dus je kan de drie stromen beschouwen als vectoren die samen een gesloten driehoek moeten vormen. Aldus heb ik de hoeken van die driehoek berekend en zo kom je te weten hoe in het geval van de topicstarter de stromen tov elkaar verdraaid moeten zijn.
De cos phi is niet gedefinieerd op basis van de fasehoek van de impedantie, maar op basis van de fasehoek tussen lijnstroom en lijnspanning. Dat is ook een maat voor de energie die verloren gaat door heen en weer pendelende stromen op het netwerk, en dat is de reden waarom grootverbruikers gaan investeren in cos phi compensatie.
De lijnspanningen aan de bron kant bij de leverancier zijn in een 3 fasig systeem mooi 120 graden tov elkaar verschoven. De stromen van de topicstarter zijn geen 120 graden verschoven (cfr. mijn berekening), dus je kan niet komen op een oplossing met cos phi gelijk aan 1. De cos phi is niet rechtstreeks gebaseerd op de faseverschuiving tussen stroom en spanning in de impedanties Z12, Z23 en Z13. Je kan met alleen weerstanden in een ongebalanceerd systeem een cos phi hebben die verschilt van 1. De cos phi kan verschillen tussen alle lijnen, dus de definitie van de cos phi voor zo een niet gebalanceerd systeem is altijd wat dubieus.
Om vermogens te berekenen zijn de 2-Wattmeter en 3-Wattmeter methodes heel interessant.
ps Je werkt met complexe getallen dus alles moeten best hoofdletters zijn.
Hopelijk kan met deze notatie de initiele opgave wat nauwkeuriger beschreven worden. Ik ben geen sterkstroomspecialist, dus het kan zijn dat er fouten instaan verbeter het dan, maar met deze notatie / terminologie wordt de discussie beter te volgen.