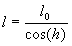9 van 9
Re: [minicursus] speciale relativiteitstheorie
Geplaatst: ma 20 jan 2014, 07:47
door descheleschilder
@Flisk: dat had ik uit #10, maar volgens de boeken is het u=(c+c)/(1+c2). Een foton dat in een met de licht reizend inertiaalstelselt met de lichtsnelheid beweegt heef toch de lichtsnelheid?
Re: [minicursus] speciale relativiteitstheorie
Geplaatst: ma 20 jan 2014, 08:11
door EvilBro
descheleschilder schreef: ↑zo 19 jan 2014, 22:59
@Evilbro: Wat gebeurt er met Δx-vΔt en Δt-vΔx/c
2 als v⇒c?
Er is niks spannends aan die limieten...
\(\lim_{v \to c} \Delta x - v \Delta t = \Delta x - c \Delta t\)
\(\lim_{v \to c} \Delta t - \frac{v \Delta x}{c^2} = \Delta t - \frac{\Delta x}{c}\)
Re: [minicursus] speciale relativiteitstheorie
Geplaatst: ma 20 jan 2014, 09:09
door physicalattraction
Een foton dat in een met de licht reizend inertiaalstelselt met de lichtsnelheid beweegt heef toch de lichtsnelheid?
Opmerking moderator
In o.a.
bericht 112 is duidelijk gemaakt dat er een inertiaalstelsel niet met de lichtsnelheid kan reizen. Elke discussie die je voortaan hier op baseert, zal direct als onwetenschappelijk worden afgekapt.
Re: [minicursus] speciale relativiteitstheorie
Geplaatst: ma 20 jan 2014, 14:43
door descheleschilder
Dat is precies wat ik wou zeggen! Elk deeltje dat in een met de lichtsnelheid bewegend inertiaalstelsel een snelheid in de richting van het IS heeft heeft tov ons de lichtsnelheid, dus ook een foton.
Re: [minicursus] speciale relativiteitstheorie
Geplaatst: ma 20 jan 2014, 15:14
door EvilBro
Dat is precies wat ik wou zeggen!
Waar is dit een reactie op?
Elk deeltje dat in een met de lichtsnelheid bewegend inertiaalstelsel een snelheid in de richting van het IS heeft heeft tov ons de lichtsnelheid, dus ook een foton.
Je kunt het blijven herhalen, maar deze zin slaat nog steeds nergens op.
Re: [minicursus] speciale relativiteitstheorie
Geplaatst: ma 20 jan 2014, 17:04
door physicalattraction
een met de lichtsnelheid bewegend inertiaalstelsel
Of nog specifieker: dit gedeelte van de zin klopt niet.
Re: [minicursus] speciale relativiteitstheorie
Geplaatst: za 22 mar 2014, 01:39
door descheleschilder
Het is wat laat, maar om even terug te komen op de limieten in de post van Evilbro van 20 januari; gaan die niet naar 0?
Re: [minicursus] speciale relativiteitstheorie
Geplaatst: za 22 mar 2014, 14:32
door EvilBro
Ja, die gaan niet naar nul (behalve in 1 specifiek geval).
Re: [minicursus] speciale relativiteitstheorie
Geplaatst: vr 11 sep 2015, 22:04
door robj
Leuke minicursus, ofschoon af en toe wel pittig en wat grote denkstappen, maar dat is niet erg.
Wel hinderlijk zijn de taalfouten: de "d" of "dt" maar ook "allebij" wat "allebei" moet zijn. Nog even een keer goed laten nakijken.
Verder niets dan lof!
Re: [minicursus] speciale relativiteitstheorie
Geplaatst: ma 14 sep 2015, 11:58
door VDammer
.
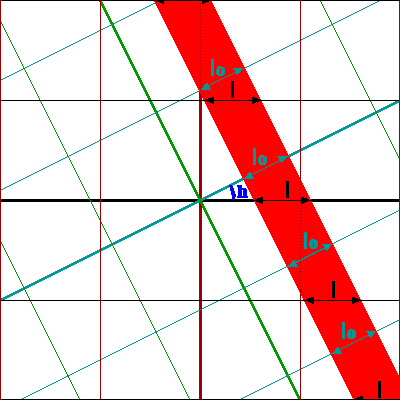
We keren nu weer terug naar de normale natuurkunde
In de figuur hierboven is de beweging van een rode staaf in de Minkowskiruimte getekend. De staaf is in rust ten opzichte van het blauw-groene coördinatenstelsel en beweegt ten opzichte van het zwart-bruine coördinatenstelsel. De lengte van de staaf is de afstand tussen de voorkant en de achterkant van de staaf op het zelfde tijdstip En gelijktijdigheid is in de twee coördinatenstelsels verschillend! De blauwe pijlen geven de lengte lo in het coördinatenstelsel in rust ten opzichte van de staaf. En de zwarte pijlen geven de lengte l in het andere coördinatenstelsel.
We zien dat
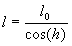
In de figuur is
l dan ook
groter dan
lo getekend, omdat er nu eenmaal geen manier is om imaginaire hoeken te tekenen.
Echter in feite is
"cos(h) = gamma.gif" groter dan 1 en
l is l0 / gamma.gif. Dit is de inmiddels bekende formule voor Lorentz lengtecontractie
Zou je hier niet beter een LOEDEL diagram tekenen?
Daarin is de wederzijdse lengteverkorting per elke ref syteem correct
korter getekend.
LOEDEL diagram is ook handiger om wederzijdse tijddilatatie correct te tekenen.
Om eerlijk te zijn... ik persoonlijk vind die mini-cursus helemaal geen 'mini' cursus'...