2 van 2
Re: Wet van behoud van impuls
Geplaatst: ma 30 aug 2010, 19:11
door bessie
Ik neem aan dat je hiermee bedoelt dat in dit topic voldoende bewijzen geleverd zijn. Ik denk ook dat dat zo is, ik voor mijzelf denk het ook wel. De twijfel die nog zou kunnen ontstaan is dat als een materiaal wordt getroffen door een stoot, de moleculen in allerlei richtingen gaan trillen, niet alleen in de richting van de stoot.
Dit is te vergelijken met een pool-biljart, waarbij die ene bal de driehoek van alle overige ballen raakt. Het lijkt of de impuls van die ene bal verloren gaat, maar in feite is het natuurlijk zo dat alle uiteenspattende ballen een beetje van zijn impuls hebben gekregen. De bewegingen loodrecht op de symmetrieas heffen elkaar netto op.
In dit (bijna) volledig elastische voorbeeld hebben de ballen samen evenveel kinetische energie als de ene bal die oorspronkelijk aan kwam rollen.
En de analogie kan nog verder gaan, na de botsing liggen door wrijving de ballen eerder stil dan dat die ene snel rollende bal afgeremd zou zijn. Ofwel de energie is gelijkgebleven op het moment van de botsing, maar wordt in zijn verspreide gedaante makkelijker gedissipeerd (ook door de toegenomen massa dus ook wrijving).
Ofwel de botsingen veranderen wel de manier waarop de energie is verdeeld, maar niet de impuls.
Re: Wet van behoud van impuls
Geplaatst: ma 30 aug 2010, 19:50
door die hanze
Ik schets even hoe ik denk dat de botsing verloopt: massa1 botst tegen de veer op massa2, die wordt ingedrukt, massa 1 oefent dus een kracht uit op de veer die op haar beurt een tegenkracht geeft naarmate ze meer wordt ingedrukt. Gevolg is dat er een rsultante op massa 1 inwerkt die m1 afremt, snelheid word kleiner. De veer geeft de kracht die m1 op haar uitoefent door naar m2, de veer oefent een kracht uit op m2 waardoor die versnelt. Op en bepaald moment zijn beide snelheden even snel en heeft de veer en m1 t.o.v elkaar geen snelheid meer, m1 oefent geen kracht meer uit op de veer maar de veer wel op massa en rekt uit, maar onmidellijk nadat dat de veer ook maar een ietsiepietse terug uitrekt treed ons fantastische mechanisme in gang en klikt de veer vast.
Gevolg: 2massa's die even snel vliegen met v'<v. Ek= v'^2.m Ep=x^2.k/2
dus E voor: Ek=v^2.m/2
E na : Ek=v'^2.m/2+Ep=x^2.k/2
=> behoud van energie
impuls voor: P=v.m
erna: P=2.m.v'
=> behoud van impuls en v' is blijkbaar 0.5v
Je hebt gelijk, alles klopt. Mijn redenerings fout was dat ik dacht dat m1 stilstond en de veer toch ingdrukt was, dit kan echter niet want als je m1 zou laten stilstaan zou de veer zich moeten ontspannen en dan moeten we ons niet afvragen waar de Ep vandaan komt.
Nu is mijn probleem met die veer opgelost maar de vraag aan het begin van het topic niet, namelijk of dat impuls niet volledig kan worden omgezet worden in warmte wat volgens mij impuls verhoging is van de deeltjes, ik beschrijf hieronder een gelijkaardig voorbeeld maar met wat vereenvoudigingen.
Stel een stuk steen met massa m (vrij klein) vliegt met een snelheid v midden in een interstellaire gaswolk die homogeen is en bijgevolg is er geen nettozwaartekracht. De steen verliest snelheid door botsing met gasmoleculen die moleculen botsen weer met anderen enzo... Uiteindelijk is de steen opgebrand of verliest hij zijn snelheid. Mijn vraag waar is de impuls? Ik denk temperatuursverhoging.
Re: Wet van behoud van impuls
Geplaatst: ma 30 aug 2010, 20:46
door Jan van de Velde
die hanze schreef:..//..
Je hebt gelijk, alles klopt. Mijn redenerings fout was dat ik dacht dat m1 stilstond en de veer toch ingdrukt was, dit kan echter niet want als je m1 zou laten stilstaan zou de veer zich moeten ontspannen en dan moeten we ons niet afvragen waar de Ep vandaan komt.
Kijk, nu ben je net overtuigd dat die wet van behoud van impuls geldig is, ongeacht energie-effecten.
Maar dan toch stug volhouden hè?
Stel een stuk steen met massa m (vrij klein) vliegt met een snelheid v midden in een interstellaire gaswolk die homogeen is en bijgevolg is er geen nettozwaartekracht. De steen verliest snelheid door botsing met gasmoleculen die moleculen botsen weer met anderen enzo... Uiteindelijk is de steen opgebrand of verliest hij zijn snelheid. Mijn vraag waar is de impuls? Ik denk temperatuursverhoging.
Nee, nee, voor de zoveelste en wat mij betreft voor de laatste maal nee, die impuls verdwijnt niet.
Zoek nou eens in die botsing steen/wolk naar mogelijkheden voor behoud van impuls waarvan je net overtuigd was. Begin voor mijn part eens te denken rond een biljartbal die een "wolk" stuiters binnenvliegt. Zie je daar behoud van impuls bij elk afzonderlijk botsinkje en dus ook in het geheel van álle optredende botsinkjes, denk dan die biljartbal eens groter en die knikkers kleiner. En daarna de biljartbal nóg groter en de knikkertjes nóg kleiner. En daarna ..... , net zolang totdat een grote steenbrok een wolk monoatomair gas binnenvliegt. Er is gewoon géén principieel verschil tussen ál die situaties.
Re: Wet van behoud van impuls
Geplaatst: ma 30 aug 2010, 21:13
door JWvdVeer
Ik denk temperatuursverhoging.
Zou best kunnen. Maar wat is temperatuur? Voor zover ik weet niets anders dan kinetische energie van de gasmoleculen (in dit geval). De impuls is daarmee nog niet verdwenen.
Re: Wet van behoud van impuls
Geplaatst: ma 30 aug 2010, 23:37
door Marko
Zou best kunnen. Maar wat is temperatuur? Voor zover ik weet niets anders dan kinetische energie van de gasmoleculen (in dit geval).
Temperatuur is de gemiddelde energie per vrijheidsgraad. Dat
kan in de beweging van gasmoleculen zitten, maar - nogmaals - dat is helemaal niet relevant. Bij een inelastische botsing wordt kinetische energie omgezet in warmte. Maar voor alle duidelijkheid, de kinetische energie wordt omgezet, niet de impuls. Impuls omzetten in energie is net zoiets als druk omzetten naar bruto nationaal product.
De impuls is daarmee nog niet verdwenen.
Vanzelfsprekend niet. Impuls is altijd behouden.
Als een steen in een interstellaire gaswolk vliegt zal die wolk, tesamen met de restanten van de steen, een snelheid hebben gekregen, voor een waarnemer die stilstond ten opzichte van de oorspronkelijke wolk.
De moleculen in die wolk bewegen ten opzichte van de gehele wolk nog steeds met zijn allen alle kanten uit.
Re: Wet van behoud van impuls
Geplaatst: za 18 dec 2010, 00:53
door die hanze
stel, je hebt 2 stenen van gelijke massa, die door een massaloos touw met elkaar verbonden zijn. Dit systeem draait rond, het bezit dus een zekere draaiimpuls. Door een of ander ingenieus systeem kunnen we het toerental van het systeem verhogen, zodat het steeds sneller en sneller begint te draaien. Op een bepaald moment zijn de spankrachten in het touw tengevolge van demiddelpuntzoekende kracht die geleverd moet worden zo groot, dat het touw breekt.
Elke steen vliegt dus met een zekere v(die aan elkaar gelijk zijn) naar elk een tegenovergestelde kant. De totale rechlijnige impuls is dus gelijk aan 0 (m.v+m.(-v)=0). Akkoord?
Natuurlijk is de draai impuls ook verdwenen. Mijn vraag is nu, wat doen we nu met wet van behoud van impuls, Waarom gaat ze nu niet meer op?
Ondertussen denk ik dat ik het antwoord weet, maar ik ben nieuwsgierig wat jullie verklaring is,.
Het topic is mss oud omdat ik er nog lange tijd over heb liggen nadenken en ben tot de conclusie gekomen dat jullie gelijk hadden maar in sommige situatie's is het toch niet simpel gloof ik. Ik zal later nog subtielere vraagjes posten.
Re: Wet van behoud van impuls
Geplaatst: za 18 dec 2010, 11:18
door physicalattraction
Ik ben het oneens met je stelling dat de totale impulsmoment nu 0 is. Ik zie niet in waarom de draaiimpuls spontaan veranderd zou zijn.
\(\overrightarrow{L} = \overrightarrow{r} \times m \overrightarrow{v}\)
, en
\(\overrightarrow{r}\)
en
\(\overrightarrow{v}\)
staan niet parallel wanneer je nog steeds dezelfde oorsprong neemt.
Re: Wet van behoud van impuls
Geplaatst: za 18 dec 2010, 13:20
door die hanze
De twee stenen vliegen met dezelfde snelheid in tegenovergestelde richting, hun snelheden zijn parralel met hun positievector vanuit hun massacentrum, ze kunnen toch on mogenlijk nog draaiimpuls hebben???
Sterker nog, stel dat we ze nog eens verbinden met een massaloos touw van 10m lang(dat veel sterker is), na een tijdje zullen de twee stenen het touw strak spannen en zullen ze abrupt gestopt worden. ze zullen dan ieder snelheid 0 hebben en dan is er helemaal geen beweging meer in het systeem en dus is de impuls zeker 0.Geen idee waar jij dan nog draaiimpuls zou vinden.
Re: Wet van behoud van impuls
Geplaatst: za 18 dec 2010, 15:09
door physicalattraction
De crux ligt hem hier dat de snelheden NIET parallel liggen aan de positievectoren. Wanneer je de snelheden zou omdraaien, zouden ze niet op elkaar botsen, maar langs elkaar suizen.
Op het moment dat het touw er nog is:
\(|L| = m \cdot |v| \cdot |r_{\perp}|\)
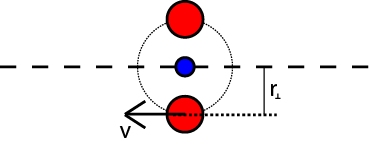
- Draaiimpuls_01 545 keer bekeken
Op het moment dat het touw er niet meer is:
\(|L| = m \cdot |v| \cdot |r_{\perp}|\)
. Niets verandert dus!
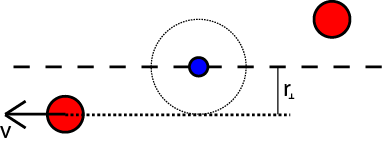
- Draaiimpuls_02 544 keer bekeken
De situatie die jij beschrijft:
\(|r_{\perp}| =0\)
, dus
\(|L| = 0\)
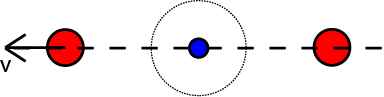
- Draaiimpuls_03 545 keer bekeken
Re: Wet van behoud van impuls
Geplaatst: za 18 dec 2010, 18:36
door die hanze
ah ik ksnap het, als je dan de ballen toch zou verbinden met een langer koord, dan zou het Systeem weer gaan draaien zodra het touw strak staat (welliswaar minder snel doordat het traagheids moment toeneemt).
Re: Wet van behoud van impuls
Geplaatst: za 18 dec 2010, 18:58
door Marko
Als het je helpt om het zo te bekijken, dan ja. Maar, touw of niet, het belangrijkste is om te onderkennen dat de snelheidsvectoren van beide stenen niet in elkaars verlengde liggen.
En het allerbelangrijkste is eigenlijk om gewoon de definitie van impulsmoment te hanteren. Opzoeken en proberen te doorgronden dus!
Re: Wet van behoud van impuls
Geplaatst: zo 19 dec 2010, 14:45
door robertus58a
Impuls en en energie (kinetisch, potentieel) worden gecombineerd in de bewegingsvergelijkingen van Lagrange:
Lagrange - mechanica
Eens de kinetische en potentieele energie beschreven zijn kan je de bewegingsvergelijkingen eenvoudig afleiden.