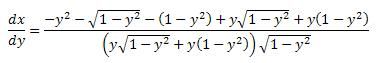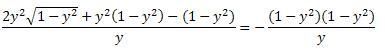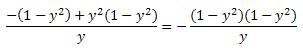sciencetalk

bramio schreef: ↑ma 01 okt 2012, 20:27

Dit is niet correct. Er ontbreekt een factor in de eerste drie termen van de teller en een factor y in de laatste twee termen van de teller.

Merk ook op dat je het jezelf moeilijk hebt gemaakt door de factoren met distributie uit te werken: je schrijft beter . Dan heb je bij het op gemeenschappelijke noemer de extra vermenigvuldiging met niet meer.

Wanneer je je breuk met de vermelde correcties uitwerkt bekom je niet de formule die je vermelde in de openingspost. De correcte afgeleide wordt gegeven door ; je kan zelf eenvoudig inzien dat de formule die je geeft niet kan kloppen door naar het teken rond 0 te kijken.

Dat laatste had ik ook gevonden, maar dat van dat teken is niet waar of beter onvolledig.
en Dus moet de functie ergens dalen op <0,1> enz.

Dat is een andere manier om het te zien. Gewoon opmerken dat de afgeleide op gegeven wordt door , is even 'waar' of 'volledig'.

Volgens mij heb ik weer een rekenfoutje gemaakt.

Ja je mist een factor in de teller:

Ok, nu klopt het wel.

Volgens mij kan ik nu beide kanten delen door (1-y^2), en daarna vermenigvuldigen met y om die breuk weg te krijgen.

Dan krijg ik:

-1+y^2=(1-y^2)

Ergens een minnetje verkeerd?

EDIT: Ja, ik zie het, op het eind ben ik een minnetje vergeten.

Heel erg bedankt voor de hulp!

Een laatste vraagje: waarom kon ik in het begin de log vervangen met een ln? 10log(x) = eln(x)?

Sommige boeken gebruiken gewoon log als ze ln bedoelen, dat geeft verwarring.