2 van 2
Re: faculteiten
Geplaatst: zo 01 jun 2014, 14:05
door mrlngtng
Safe schreef:
Nee met een ?-teken ...
n!/(k!(n-k)!)
zie je het verschil?
Wat wordt nu:
\(\left({2k\choose k}\right)^{-1}\)
Nee ik ben niet mee met de redenering?
Re: faculteiten
Geplaatst: zo 01 jun 2014, 14:35
door Safe
Welke redenering ...
Re: faculteiten
Geplaatst: zo 01 jun 2014, 14:37
door mrlngtng
Safe schreef:
Welke redenering ...
Ik snap niet waar je naartoe wilt.
Ik weet dat de definitie : n! / k! (n-k)!.
Maar wat dan?
Re: faculteiten
Geplaatst: zo 01 jun 2014, 14:51
door Safe
mrlngtng schreef:
Ik weet dat de definitie : n! / k! (n-k)!.
Je schrijft de definitie verkeerd op (kijk naar m'n post en de vraag daarbij!) ...
Wat is a^-1?
Re: faculteiten
Geplaatst: zo 01 jun 2014, 15:47
door mrlngtng
Safe schreef:
Je schrijft de definitie verkeerd op (kijk naar m'n post en de vraag daarbij!) ...
Wat is a^-1?
a^-1 = 1/a ?
Dus dan is het toch:
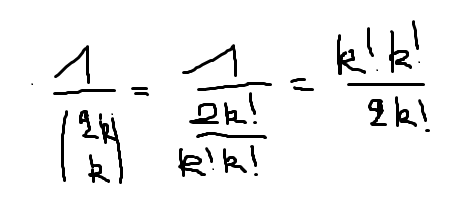
- Naamloos 502 keer bekeken
Of niet?
Re: faculteiten
Geplaatst: zo 01 jun 2014, 22:41
door Safe
Prima!
Ga verder ...
Re: faculteiten
Geplaatst: ma 02 jun 2014, 10:26
door mrlngtng
Safe schreef:
Prima!
Ga verder ...
Oke, als ik dan hiervoor de convergentie wil aantonen bekom ik L = 1/4, dus de reeks is convergent. Klopt dat?
Re: faculteiten
Geplaatst: ma 02 jun 2014, 11:50
door Safe
Welke reeks? Ben je met machtreeksen bezig ...
Re: faculteiten
Geplaatst: ma 02 jun 2014, 11:57
door mrlngtng
Safe schreef:
Welke reeks? Ben je met machtreeksen bezig ...
Safe schreef:
Welke reeks? Ben je met machtreeksen bezig ...
Het is de bedoeling om via de verhoudingstest (Alembert) de convergentie te onderzoeken van deze reeks, net zoals bij het vorige voorbeeld.
Re: faculteiten
Geplaatst: ma 02 jun 2014, 12:11
door Drieske
Je reeks is dus
\(\sum \left({2k \choose k}\right)^{-1}\)
en
\(L = \lim_{k \to \infty} \frac{a_{k+1}}{a_k}?\)
Dan klopt L = 1/4.
Re: faculteiten
Geplaatst: ma 02 jun 2014, 13:46
door mrlngtng
Oke, bedankt allemaal!
Re: faculteiten
Geplaatst: ma 02 jun 2014, 15:53
door Safe
Maar je bent ook met machtreeksen bezig ... ?