2 van 3
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 14:11
door tempelier
Ik heb hem ook op de ruwe en brute manier gevonden dat x+y=2
(Omgezet naar een zesdegraads vergelijking in x.)
Blijf voor de andere oplossingen zitten met een vierde graadsvergelijking.
Ik denk dat die ook mooie oplossingen moet hebben gezien het antwoord van ukster.
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 14:13
door tempelier
ukster schreef: ↑zo 01 aug 2021, 14:01
Xilvo schreef: ↑zo 01 aug 2021, 13:25
Mooi! Zelf gevonden?
Nee 
De uitwerking op zichzelf is doodsimpel..
maar kom er maar eens op!
Ik kan me (nog) geen voorstelling maken bij zo'n complex snijpunt.
Misschien vinden we hierin het antwoord
visualizing complex roots.pdf
x+y= q had ik zelf bedacht na heel veel rommelen kwam ik er ook op.
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 14:39
door Xilvo
ukster schreef: ↑zo 01 aug 2021, 14:01
De uitwerking op zichzelf is doodsimpel..
maar kom er maar eens op!
Net als met jouw integraal van afgelopen week. De oplossing was goed te volgen maar hoe kom je op zo'n gedachtesprong.
ukster schreef: ↑zo 01 aug 2021, 14:01
Ik kan me (nog) geen voorstelling maken bij zo'n complex snijpunt.
Misschien vinden we hierin het antwoord
visualizing complex roots.pdf
In ieder geval niet helemaal. Het construeren maakt het voor mij niet helderder dan het berekenen.
Bovendien heb je bij een nulpunt alleen te maken met een complexe x-waarde, de y-waarde is dan altijd nul.
Bij het snijpunt van twee krommen kun je te maken krijgen met zowel een complexe x- als een complexe y-waarde.
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 14:53
door tempelier
Nu je over integreren begint.
Bij dubbel integralen wordt dit type substitutie nog al eens gebruikt.
Maar ja, dat is achteraf makkelijk gezegd.
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 15:38
door Xilvo
Xilvo schreef: ↑zo 01 aug 2021, 13:25
Of is dat een andere dimensie, wat het een vierdimensionaal vraagstuk maakt? Ik vermoed het laatste.
Natuurlijk is het vierdimensionaal. Reële en imaginaire deel van x, idem voor y.
Voor de snijpunten van y=x
2+5 en y=2x vind je x=1±2i, met y=2±4i.
In vier dimensies zijn dat de punten (1,2,2,4) en (1,-2,2,-4), met e
1 = Re(x), e
2 = Im(x), e
3 = Re(y), e
4 = Im(y).
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 19:56
door ukster
4D is nogal wat!
Met betrekking tot het topicvraagstuk probeer ik me vooral niets voor te stellen bij complexe snijpunten.
Wel zie ik dat een rechte x+y=c welke geen raakpunt of snijpunten heeft met de grafiek van
x
2+y
2=c1 en x
3+y
3=c2 leidt tot een complexe waarde voor x1,x2 en y1,y2 welke vervolgens ingevuld in beide formules altijd een reële uitkomst geeft zodat de vergelijkingen kloppen.
x en y (elkaars toegevoegd complexe) kunnen toch gewoon gesuperponeerd met de grafieken worden weergeven in het 2D vlak?
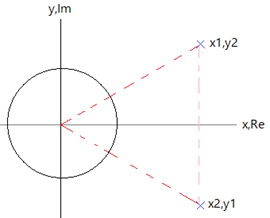
- toegevoegd complex 1016 keer bekeken
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 20:15
door Xilvo
ukster schreef: ↑zo 01 aug 2021, 19:56
4D is nogal wat!
Ja. Dat maakt het lastig/onmogelijk het voor te stellen.
ukster schreef: ↑zo 01 aug 2021, 19:56
x en y (elkaars toegevoegd complexe) kunnen toch gewoon gesuperponeerd met de grafieken worden weergeven in het 2D vlak?
Dat lijkt me niet goed. Zowel x als y zijn complex, je mist volgens mij twee dimensies in de tekening.
y is niet het imaginaire deel van een getal.
Of ik begrijp de tekening niet goed.
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 20:19
door ukster
ik zie het als toegevoegd complexe vectoren
y2=x1=a+jb
y1=x2=a-jb
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 20:25
door Xilvo
ukster schreef: ↑zo 01 aug 2021, 20:19
ik zie het als toegevoegd complexe vectoren
y2=x1=a+jb
y1=x2=a-jb
Maar dat zijn dan geen punten in het vlak van de cirkel, de kromme en de rechten?
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 20:31
door ukster
Welke grafische voorstelling heb jij dan voor ogen?
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 20:43
door Xilvo
ukster schreef: ↑zo 01 aug 2021, 20:31
Welke grafische voorstelling heb jij dan voor ogen?
Dat is nou precies het probleem. Het zou een voorstelling van een 4-dim ruimte moeten zijn.
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 20:50
door ukster
Een vierdimensionale ruimte is een wiskundige uitbreiding van het concept van driedimensionale of 3D-ruimte lees ik zojuist. Lijkt me een aardig onderwerp om eens flink in te duiken

Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 21:12
door ukster
Was het niet zo dat je een array elke dimensie kunt geven die je maar wil?
Is dit je idee?
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 21:29
door Xilvo
ukster schreef: ↑zo 01 aug 2021, 21:12
Was het niet zo dat je een array elke dimensie kunt geven die je maar wil?
Is dit je idee?
Ja, zoals ik hierboven schreef:
Voor de snijpunten van y=x2+5 en y=2x vind je x=1±2i, met y=2±4i.
In vier dimensies zijn dat de punten (1,2,2,4) en (1,-2,2,-4), met e1 = Re(x), e2 = Im(x), e3 = Re(y), e4 = Im(y).
Re: vergelijkingen
Geplaatst: ma 02 aug 2021, 08:09
door tempelier
Xilvo schreef: ↑zo 01 aug 2021, 13:25
Mooi! Zelf gevonden?
Ik kan me (nog) geen voorstelling maken bij zo'n complex snijpunt.
De x-as kan je uitbreiden tot een complex vlak met de imaginaire richting loodrecht op het papier. Zeg maar de z-richting.
Idem voor de y-as. Maar is dat diezelfde z-richting, waardoor het een driedimensionaal probleem wordt?
Of is dat een andere dimensie, wat het een vierdimensionaal vraagstuk maakt? Ik vermoed het laatste.
Er zijn geen complexe snijpunten.
Zouden ze toch gevonden worden als oplossingen dan moeten ze geskipt worden omdat ze buiten de Horizon vallen.
------------------------------
Wil je een andere Horizon ZELF invoerendan kan dat natuurlijk maar bedenk wel dat je dan eerst moet vermelden wat er met de omschrijvingen wordt bedoeld.
PS.
Meestal wordt er dan met banen gewerkt.