Professor Puntje schreef: ↑zo 08 aug 2021, 18:02
1. Is het aannemelijk om van dezelfde kracht T bij bakje A en bakje B uit te gaan.
Laten we eens zien wat er gebeurt als we daar
niet van uitgaan. Hier een aangepast bewijs waarbij de terugslagkrachten bij bakje A en bakje B niet als gelijk zijn aangenomen:
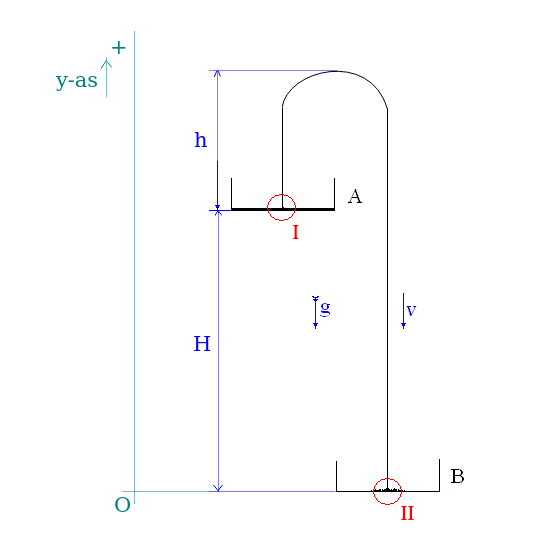
- ketting-nieuw 1194 keer bekeken
In de stationaire situatie beweegt het zwaartepunt van de ketting eenparig rechtlijnig zodat de som van de externe krachten op de ketting dan nul moet zijn. Laat S
A de trekkracht in de ketting vlak boven bakje A zijn, en μ
A de verhouding tussen de terugslagkracht T vanuit bakje A op de vertrekkende schakels van de ketting en de trekkracht S
A. Omdat in bakje B het omgekeerde gebeurt trekt daar een kracht U aan de daar aankomende ketting. We nemen aan dat U = μ
Bλv
2 , zodat de terugslagkracht U vlak boven bakje B recht evenredig is met de kracht die de neerkomende ketting op bakje B uitoefent. Laat verder M de totale massa van de ketting zijn, en m
A de massa van de ketting in bakje A, en m
B de massa van de ketting in bakje B. De lineaire dichtheid van de ketting noemen we λ. De totale opwaartse kracht F
A in bakje A op de ketting is dan:
\(\)
\( F_A = m_A \, \mathrm{g} + T \)
\(\)
\( F_A = m_A \, \mathrm{g} + \mu_A S_A \,\,\,\,\,\, \mathrm{(I)} \)
\(\)
De opwaartse kracht F
B in bakje B op de ketting is:
\(\)
\( F_B = m_B \, \mathrm{g} + \frac{v \mathrm{d}t \lambda v}{ \mathrm{d} t} \)
\(\)
\( F_B = m_B \, \mathrm{g} + \lambda v^2 \,\,\,\,\,\,\, \mathrm{(II)} \)
\(\)
Verder werkt op de ketting als geheel nog de zwaartekracht F
M:
\(\)
\( F_M = - \mathrm{M} \mathrm{g} \,\,\,\,\,\,\,\,\, \mathrm{(III)} \)
\(\)
Dus moet gelden:
\(\)
\( F_A + F_B + F_M = 0 \,\,\,\,\,\,\,\,\, \mathrm{(IV)} \)
\(\)
\( m_A \, \mathrm{g} + \mu_A S_A + m_B \, \mathrm{g} + \lambda v^2 - \mathrm{M} \mathrm{g} = 0 \)
\(\)
\( (m_A + m_B - \mathrm{M}) \mathrm{g} + \mu_A S_A + \lambda v^2 = 0 \)
\(\)
\( - (\mathrm{H} + 2 h) \lambda \mathrm{g} + \mu_A S_A + \lambda v^2 = 0 \,\,\,\,\,\,\,\,\, \mathrm{(V)} \)
\(\)
Voor bakje A waar de ketting in beweging wordt gebracht hebben we nog:
\(\)
\( S_A + T = \frac{ v \mathrm{d}t \lambda v}{\mathrm{d}t} \)
\(\)
\( S_A + T = \lambda v^2 \)
\(\)
\( S_A + \mu_A S_A = \lambda v^2 \)
\(\)
\( (1 +\mu_A) S_A = \lambda v^2 \,\,\,\,\,\,\,\,\, \mathrm{(VI)}\)
\(\)
\( S_A = \frac{\lambda v^2}{1 + \mu_A} \,\,\,\,\,\,\,\,\, \mathrm{(VII)} \)
\(\)
Zodat wegens (V) en (VII) geldt:
\(\)
\( - (\mathrm{H} + 2 h) \lambda \mathrm{g} + \frac{\mu_A \lambda v^2}{1 + \mu_A} + \lambda v^2 = 0 \)
\(\)
\( \frac{\mu_A \lambda v^2}{1 + \mu_A} + \lambda v^2 = (\mathrm{H} + 2 h) \lambda \mathrm{g} \)
\(\)
\( \frac{\mu_A v^2}{1 + \mu_A} + v^2 = (\mathrm{H} + 2 h) \mathrm{g} \)
\(\)
\( \left ( \frac{\mu_A}{1 + \mu_A} + 1 \right ) v^2 = (\mathrm{H} + 2 h) \mathrm{g} \)
\(\)
\( \left ( \frac{\mu_A}{1 + \mu_A} + \frac{1 + \mu_A}{1 + \mu_A} \right ) v^2 = (\mathrm{H} + 2 h) \mathrm{g} \)
\(\)
\( \frac{1 + 2 \mu_A}{1 + \mu_A} v^2 = (\mathrm{H} + 2 h) \mathrm{g} \,\,\,\,\,\,\,\,\, \mathrm{(VIII)} \)
\(\)
Vanwege de stationaire situatie hebben we ook:
\(\)
\( S_A = \mathrm{H} \lambda \mathrm{g} + U \)
\(\)
\( S_A = \mathrm{H} \lambda \mathrm{g} + \mu_B \lambda v^2 \)
\(\)
En dus wegens (VI) dat:
\(\)
\( S_A = \mathrm{H} \lambda \mathrm{g} + \mu_B (1 +\mu_A) S_A \)
\(\)
\( (1 - \mu_B (1 +\mu_A) ) S_A = \mathrm{H} \lambda \mathrm{g} \)
\(\)
\( S_A = \frac{\mathrm{H} \lambda \mathrm{g}}{ 1 - \mu_B (1 +\mu_A) } \,\,\,\,\,\,\,\,\, \mathrm{(IX)} \)
\(\)
Zodat wegens (VII) en (IX):
\(\)
\( \frac{\lambda v^2}{1 + \mu_A} = \frac{\mathrm{H} \lambda \mathrm{g}}{ 1 - \mu_B (1 +\mu_A) } \)
\(\)
\( \frac{v^2}{1 + \mu_A} = \frac{\mathrm{H} \mathrm{g}}{ 1 - \mu_B (1 +\mu_A) } \)
\(\)
\( v^2 = \frac{1 + \mu_A}{ 1 - \mu_B (1 +\mu_A) } \mathrm{H} \mathrm{g} \,\,\,\,\,\,\,\,\, \mathrm{(X)} \)
\(\)
Combinatie van (VIII) en (X) geeft:
\(\)
\( \frac{1 + 2 \mu_A}{1 + \mu_A} \frac{1 + \mu_A}{ 1 - \mu_B (1 +\mu_A) } \mathrm{H} \mathrm{g} = (\mathrm{H} + 2 h) \mathrm{g} \)
\(\)
\( \frac{ 1 + 2 \mu_A }{ 1 - \mu_B (1 +\mu_A) } \mathrm{H} \mathrm{g} = (\mathrm{H} + 2 h) \mathrm{g} \)
\(\)
\( \frac{ 1 + 2 \mu_A }{ 1 - \mu_B (1 +\mu_A) } \mathrm{H} = \mathrm{H} + 2 h \)
\(\)
\( \frac{ 1 + 2 \mu_A }{ 1 - \mu_B (1 +\mu_A) } \mathrm{H} - \mathrm{H} = 2 h \)
\(\)
\( \left ( \frac{ 1 + 2 \mu_A }{ 1 - \mu_B (1 +\mu_A) } - 1 \right ) \mathrm{H} = 2 h \)
\(\)
\( \left ( \frac{ 1 + 2 \mu_A }{ 1 - \mu_B (1 +\mu_A) } - \frac{ 1 - \mu_B (1 +\mu_A) }{ 1 - \mu_B (1 +\mu_A) } \right ) \mathrm{H} = 2 h \)
\(\)
\( \frac{ 2 \mu_A + \mu_B (1 +\mu_A) }{ 1 - \mu_B (1 +\mu_A) } \mathrm{H} = 2 h \)
\(\)
\( h \, = \, \frac{1}{2} \, \frac{ 2 \mu_A + \mu_B (1 +\mu_A) }{ 1 - \mu_B (1 +\mu_A) } \, \mathrm{H} \,\,\,\,\,\,\,\,\, \mathrm{(XI)} \)
\(\)