2 van 2
Re: state space
Geplaatst: ma 12 jun 2023, 12:26
door ukster
ik blijf het vreemd vinden.

- netwerk 2039 keer bekeken
ik gebruik voor dit netwerk geen initial conditions (volgens mij default nul)
de responsplot
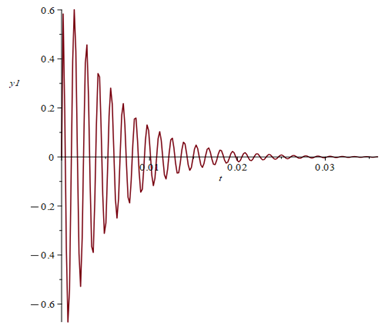
- stapresponsie 2039 keer bekeken
vanuit het state space model
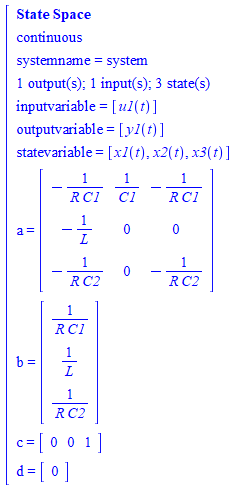
- statespacemodel 2037 keer bekeken
en is exact gelijk aan die van het professionele simulatiesoftwarepakket
Microcap (stapresponsie 1V)
Re: state space
Geplaatst: ma 12 jun 2023, 12:38
door ukster
met de toestandsvariabelen:

- toestandsvariabelen 2029 keer bekeken
Re: state space
Geplaatst: ma 12 jun 2023, 12:38
door Xilvo
Voor de eerste afgeleide krijg ik 2409,7, voor x 208,5
Heb je niet toevallig de verkeerde variable geplot?
(ik heb me verder nog niet in het model verdiept).
Re: state space
Geplaatst: ma 12 jun 2023, 12:59
door ukster
Nee,

- 1 2028 keer bekeken

- 2 2027 keer bekeken
Re: state space
Geplaatst: ma 12 jun 2023, 17:38
door wnvl1
Dit krijg ik met het Matlab State Space model.
Code: Selecteer alles
A = [0, 1, 0; 0,0, 1; 12, -6, 9];
B = [0;0;3];
C = [0,1,0];
D = [0];
x0 = [0 ; 0; 0];
sys = ss(A,B,C,D)
initial(sys,x0)
t = 0:0.00001:1;
u = heaviside(t);
lsimplot(sys,u,t)
grid on
Re: state space
Geplaatst: ma 12 jun 2023, 17:43
door wnvl1
Als ik het juist begrijp, dan correspondeert mijn oplossing met de state space oplossing van Ukster in Maple, maar niet met de oplossing van Xilvo en Ukster als ze gewoon de DV oplossen.
Re: state space
Geplaatst: ma 12 jun 2023, 20:46
door ukster

- rootlocusplot 1984 keer bekeken
Het is een instabiel systeem. zou dat een verklaring voor het verschil kunnen zijn?
Re: state space
Geplaatst: ma 12 jun 2023, 22:58
door wnvl1
Instabiel systeem betekent positieve eigenwaarden, maar dat verandert echt niks aan het feit dat beide oplossingen tot hetzelfde zouden moeten leiden. Ik zal later verder zoeken. De homogene is ook gemakkelijk analytisch met de hand op te lossen. Ik zal dat later hier posten.
Re: state space
Geplaatst: wo 14 jun 2023, 20:17
door wnvl1
Eventjes symbolisch met matlab het homogene systeem opgelost.
Code: Selecteer alles
syms x1(t) x2(t) x3(t)
ode1 = diff(x1) == x2;
ode2 = diff(x2) == x3;
ode3 = diff(x3) == 12*x1 - 6*x2 + 9*x3;
odes = [ode1; ode2;, ode3]
S=dsolve(odes)
simplify(S.x1)
simplify(S.x2)
simplify(S.x3)
Het zijn wel hele lange antwoorden.
x_1 =
C2*(sin((3^(1/2)*t*((233^(1/2) + 24)^(1/3) - (24 - 233^(1/2))^(1/3)))/2)*exp(-t*((233^(1/2) + 24)^(1/3)/2 + (24 - 233^(1/2))^(1/3)/2 - 3))*((699^(1/2)*(24 - 233^(1/2))^(2/3))/2352 - (25*3^(1/2)*(24 - 233^(1/2))^(2/3))/2352 + ((17*3^(1/2) + 699^(1/2))*(24 - 233^(1/2))^(1/3))/336) - exp(-t*((233^(1/2) + 24)^(1/3)/2 + (24 - 233^(1/2))^(1/3)/2 - 3))*cos((3^(1/2)*t*((233^(1/2) + 24)^(1/3) - (24 - 233^(1/2))^(1/3)))/2)*((233^(1/2)*(24 - 233^(1/2))^(1/3))/336 - (233^(1/2)*(24 - 233^(1/2))^(2/3))/2352 + (17*(24 - 233^(1/2))^(1/3))/336 + (25*(24 - 233^(1/2))^(2/3))/2352 + 5/12)) - C3*(exp(-t*((233^(1/2) + 24)^(1/3)/2 + (24 - 233^(1/2))^(1/3)/2 - 3))*cos((3^(1/2)*t*((233^(1/2) + 24)^(1/3) - (24 - 233^(1/2))^(1/3)))/2)*((699^(1/2)*(24 - 233^(1/2))^(2/3))/2352 - (25*3^(1/2)*(24 - 233^(1/2))^(2/3))/2352 + ((17*3^(1/2) + 699^(1/2))*(24 - 233^(1/2))^(1/3))/336) + sin((3^(1/2)*t*((233^(1/2) + 24)^(1/3) - (24 - 233^(1/2))^(1/3)))/2)*exp(-t*((233^(1/2) + 24)^(1/3)/2 + (24 - 233^(1/2))^(1/3)/2 - 3))*((233^(1/2)*(24 - 233^(1/2))^(1/3))/336 - (233^(1/2)*(24 - 233^(1/2))^(2/3))/2352 + (17*(24 - 233^(1/2))^(1/3))/336 + (25*(24 - 233^(1/2))^(2/3))/2352 + 5/12)) + C4*exp(t*((233^(1/2) + 24)^(1/3) + (24 - 233^(1/2))^(1/3) + 3))*((233^(1/2)*(24 - 233^(1/2))^(1/3))/168 - (233^(1/2)*(24 - 233^(1/2))^(2/3))/1176 + (17*(24 - 233^(1/2))^(1/3))/168 + (25*(24 - 233^(1/2))^(2/3))/1176 - 5/12)
x_2=
C2*(sin((3^(1/2)*t*((233^(1/2) + 24)^(1/3) - (24 - 233^(1/2))^(1/3)))/2)*exp(-t*((233^(1/2) + 24)^(1/3)/2 + (24 - 233^(1/2))^(1/3)/2 - 3))*((23*3^(1/2)*(24 - 233^(1/2))^(2/3))/1176 + (699^(1/2)*(24 - 233^(1/2))^(2/3))/392 + ((3*3^(1/2) + 699^(1/2))*(24 - 233^(1/2))^(1/3))/168) + exp(-t*((233^(1/2) + 24)^(1/3)/2 + (24 - 233^(1/2))^(1/3)/2 - 3))*cos((3^(1/2)*t*((233^(1/2) + 24)^(1/3) - (24 - 233^(1/2))^(1/3)))/2)*((233^(1/2)*(24 - 233^(1/2))^(2/3))/392 - (233^(1/2)*(24 - 233^(1/2))^(1/3))/168 - (24 - 233^(1/2))^(1/3)/56 + (23*(24 - 233^(1/2))^(2/3))/1176 + 1/6)) - C3*(exp(-t*((233^(1/2) + 24)^(1/3)/2 + (24 - 233^(1/2))^(1/3)/2 - 3))*cos((3^(1/2)*t*((233^(1/2) + 24)^(1/3) - (24 - 233^(1/2))^(1/3)))/2)*((23*3^(1/2)*(24 - 233^(1/2))^(2/3))/1176 + (699^(1/2)*(24 - 233^(1/2))^(2/3))/392 + ((3*3^(1/2) + 699^(1/2))*(24 - 233^(1/2))^(1/3))/168) - sin((3^(1/2)*t*((233^(1/2) + 24)^(1/3) - (24 - 233^(1/2))^(1/3)))/2)*exp(-t*((233^(1/2) + 24)^(1/3)/2 + (24 - 233^(1/2))^(1/3)/2 - 3))*((233^(1/2)*(24 - 233^(1/2))^(2/3))/392 - (233^(1/2)*(24 - 233^(1/2))^(1/3))/168 - (24 - 233^(1/2))^(1/3)/56 + (23*(24 - 233^(1/2))^(2/3))/1176 + 1/6)) + C4*exp(t*((233^(1/2) + 24)^(1/3) + (24 - 233^(1/2))^(1/3) + 3))*((233^(1/2)*(24 - 233^(1/2))^(1/3))/84 - (233^(1/2)*(24 - 233^(1/2))^(2/3))/196 + (24 - 233^(1/2))^(1/3)/28 - (23*(24 - 233^(1/2))^(2/3))/588 + 1/6)
x_3=
exp(-t*((233^(1/2) + 24)^(1/3)/2 + (24 - 233^(1/2))^(1/3)/2 - 3))*(C2*cos((3^(1/2)*t*((233^(1/2) + 24)^(1/3) - (24 - 233^(1/2))^(1/3)))/2) + C4*exp(t*((3*(233^(1/2) + 24)^(1/3))/2 + (3*(24 - 233^(1/2))^(1/3))/2)) + C3*sin((3^(1/2)*t*((233^(1/2) + 24)^(1/3) - (24 - 233^(1/2))^(1/3)))/2))
Re: state space
Geplaatst: wo 14 jun 2023, 20:21
door wnvl1
Als je dit met de hand wil doen, dan verloopt dat via de eigenwaarden en eigenvectoren van A, die je kan herkennen in de oplossing.
De positieve reële delen van de eigenwaarden wijzen erop dat het systeem instabiel is.
Om de niet homogene DV op te lossen kan je werken met bvb variatie van parameters. Dat principe is uitbreidbaar naar stelsels van DV's. Die integralen gaan voor een stapfunctie u in het rechterlid volgens mij analytisch oplosbaar zijn.
Re: state space
Geplaatst: wo 14 jun 2023, 20:33
door wnvl1
Probleem is dat op het niet-homogene systeem matlab blijft hangen. Ik heb even gewerkt met 3 ipv met een stapfunctie om het iets eenvoudiger te maken.
Code: Selecteer alles
syms x1(t) x2(t) x3(t)
ode1 = diff(x1) == x2;
ode2 = diff(x2) == x3;
ode3 = diff(x3) == 12*x1 - 6*x2 + 9*x3 + 3;
odes = [ode1; ode2;, ode3]
S=dsolve(odes)
simplify(S.x1)
simplify(S.x2)
simplify(S.x3)
Re: state space
Geplaatst: wo 14 jun 2023, 21:57
door wnvl1
Maar als ik het gewooon oplos in Python met odeint, dan kom ik dezelfde oplossing uit als in mijn statemodel.
Dat doet mij vermoeden dat er met het state spacemodel niets mis is.
Kan het zijn dat de fout eerder zit in jullie alternatieve oplossing?
Code: Selecteer alles
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
x1=0
x2=0
x3=0
def dxdt(X, t):
x1, x2, x3 = X
dx1dt = x2
dx2dt = x3
dx3dt = 12*x1 - 6*x2 + 9*x3 + 3
return dx1dt, dx2dt, dx3dt
t = np.linspace(0, 1, 1000000)
X0 = x1, x2, x3
sol = odeint(dxdt, X0, t)
print (sol)
plt.plot(t, sol[:, 0], 'r', label='x1(t)')
plt.plot(t, sol[:, 1], 'g', label='x2(t)')
plt.plot(t, sol[:, 2], 'b', label='x3(t)')
plt.legend(loc='best')
plt.xlabel('t')
plt.grid()
plt.show()