2 van 2
Re: Dwarskrachten.
Geplaatst: zo 24 feb 2008, 19:55
door Sjakko
Bij je laatste tekening haal je opeens krachten weg. Waarom?
De verdeelde belasting oefent naar beneden een kracht uit van qx met x de lengte van het balkje. De Reactiekracht in het rechter oplegpunt is gelijk aan qL/2 en die is omhoog gericht. Aangezien je rechts van het midden zit, geldt x<L/2 dus qx<qL/2 ofwel: de resultante kracht werkt naar boven! De uitwendige kracht (aan het snede) moet dus naar beneden gericht zijn.
Re: Dwarskrachten.
Geplaatst: ma 25 feb 2008, 07:37
door oktagon
Ik heb me niet helemaal verdiept over de uitleg die de topichouder zou kunnen helpen over een dwarskrachtenlijn en zal pogen om het zo eenvoudige mogelijk te doen:
Een dwarskrachtenlijn is een grafische voorstelling van optredende dwarskrachten -in dit geval- in een balk door alle optredende krachten op het zg."vrije lichaam"van die balk .
Dus door oplegreacties en balklasten en eigengewicht.
Als je dus begint met het tekenen en we beginnen meestal uiterst links op een zg.horizontale nullijn,dan zetten we de linker oplegreactie in een naar boven gerichte lijn,conform de werkelijkheid.
Vervolgens gaan we vanuit dit hoogste punt een naar beneden afnemende lijn te tekenen en dat kun je dus doen per hele kleine stukjes afnemende kracht,je kunt bij een gelijkmatige belasting uitgaan van het feit,dat die halve balkbelasting gelijk is aan de linker oplegreactie.
De schuine lijn komt dan in het midden uit op de nullijn en duikt in gelijke richting beneden de nullijn en komt op de "vector"van de rechter oplegreactie terecht,het laagste punt van de schuine lijn.
Als je dan vanaf dat punt de lijn naar boven volgt of tekent heb je de waarde van de rechter oplegreactie.
Het volgende verhaal geldt in de sterkteleer:"Daar waar die ( schuine) dwarskracht de nullijn passeert,is het moment maximaal "en kun je berekenen,door het opp.van dat dwarskrachtenvlak ter linkerzijde van de nullijnpassage te berekenen. (nb.Bij gevarieerde belastingen met verschillende belastingen/steunpunten moet je bij elke nullijnpassage de som van de oppervlakken nemen en de vlakken boven de nullijn als positief en die eronder als negatief nemen.
Maar dat is een kwestie van afspraak in het systeem,kan ook andersom,maar je moet wel konsekwent blijven in een systeem!
Re: Dwarskrachten.
Geplaatst: ma 25 feb 2008, 14:07
door willem1
mss dat volgende jullie kan duidelijk maken waar ik mis zit, ik zie het niet meer:
Als we de (blauwe) balk doorzagen in allemaal kleine stukjes (in dit voorbeeld in slechts zes stukken), kunnen we op elke doorsnede de dwarskrachten weergeven die op het snijvlak van die doorsnede is.
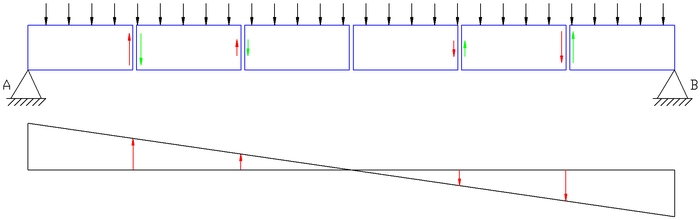
- Drawing1 398 keer bekeken
De rode pijl geeft de kracht aan die de linkerzijde van de doorsnede uitoefent op de rechterzijde. De groene pijl geeft de kracht aan die de rechterzijde uitoefent op de linkerzijde. Deze rode pijlen kunnen we daarna weergeven in de krachtenlijn.
Hoop dat deze tekening nu wat duidelijkheid geeft.
Oh ja , in de tekening zijn de moment(krachten) niet weergegeven, daar het hier zuiver om de dwarskrachten gaat.
Re: Dwarskrachten.
Geplaatst: ma 25 feb 2008, 17:08
door Bert F
Bedankt allemaal ik denk dat ik het begrijp. Mss dat ik nog wat voorbeeldjes zelf ga proberen te maken om met wat te oefenen helaas heb ik de oplossingen niet. Groeten
Re: Dwarskrachten.
Geplaatst: ma 25 feb 2008, 21:51
door Sjakko
Bedankt allemaal ik denk dat ik het begrijp. Mss dat ik nog wat voorbeeldjes zelf ga proberen te maken om met wat te oefenen helaas heb ik de oplossingen niet. Groeten
Krachtenevenwicht op het overblijvende balkdeel geeft je de oplossing.
Re: Dwarskrachten.
Geplaatst: di 26 feb 2008, 18:02
door Bert F
Oké bedankt.