- ukster
- Artikelen: 0
- Berichten: 4.917
- Lid geworden op: za 28 nov 2015, 10:42
Re: maximaal vermogen
Geweldig, aan deze oplossing had ik (nog) niet gedacht. kort en krachtige uitleg. chapeau!
- Professor Puntje
- Artikelen: 0
- Berichten: 7.574
- Lid geworden op: vr 23 okt 2015, 23:02
Re: maximaal vermogen
@ EvilBro
Dat is een slimme oplossing!
Ik zal nog eens kijken of het dan toch ook via de door WillemB aangegeven weg kan, ik liep daarbij vast. Maar misschien zie je ook hoe dat dan moet.
Dat is een slimme oplossing!
Ik zal nog eens kijken of het dan toch ook via de door WillemB aangegeven weg kan, ik liep daarbij vast. Maar misschien zie je ook hoe dat dan moet.
- WillemB
- Artikelen: 0
- Berichten: 654
- Lid geworden op: do 20 feb 2014, 17:51
Re: maximaal vermogen
Was toch benieuwd als ik het uitreken op zijn boerenfluitjes in excel met 54, 540 en 5400 punten grafiek, met 3 tau =5,4 milliSec.
voor de spannings vorm: :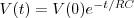
Begin spanning 50 Volt, tijd 5,4 mS, en eindspanning 2,48 Volt
ik kwam met 54 punten uit op 9,07 mA
met 540 punten op 8,8 mA
en met 5400 punten ook op 8,8 mA
Nu de vraag hoe kan dit , wat doe ik dan fout als het volgens de integraal berekening 11,3 mA oplevert ...???
Had toch ergens in de zelfde buurt moeten uitkomen met statistiek.
voor de spannings vorm: :
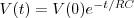
Begin spanning 50 Volt, tijd 5,4 mS, en eindspanning 2,48 Volt
ik kwam met 54 punten uit op 9,07 mA
met 540 punten op 8,8 mA
en met 5400 punten ook op 8,8 mA
Nu de vraag hoe kan dit , wat doe ik dan fout als het volgens de integraal berekening 11,3 mA oplevert ...???
Had toch ergens in de zelfde buurt moeten uitkomen met statistiek.
Sinds de uitvinding van tijd, hebben we het niet meer, en kunnen we het ook niet meer vinden.
En wie haast heeft moet langzamer lopen.
En wie haast heeft moet langzamer lopen.
- WillemB
- Artikelen: 0
- Berichten: 654
- Lid geworden op: do 20 feb 2014, 17:51
Re: maximaal vermogen
Ik heb het verschil gevonden,
het gemiddelde van de som de stromen van 540 punten geetf 8,8 mA, en dan 140 mWatt
het gemiddelde van de som der kwadraten van 540 punten geeft 232 mWatt
nog iets om over na te denken
het gemiddelde van de som de stromen van 540 punten geetf 8,8 mA, en dan 140 mWatt
het gemiddelde van de som der kwadraten van 540 punten geeft 232 mWatt
nog iets om over na te denken
Sinds de uitvinding van tijd, hebben we het niet meer, en kunnen we het ook niet meer vinden.
En wie haast heeft moet langzamer lopen.
En wie haast heeft moet langzamer lopen.
- Professor Puntje
- Artikelen: 0
- Berichten: 7.574
- Lid geworden op: vr 23 okt 2015, 23:02
Re: maximaal vermogen
@ WillemB
Zo moet het toch ook:
Zo moet het toch ook:
\( \mbox{P}_{gem} = \frac{1}{\mbox{T}} \, \int_0^T \mbox{P}(t) \, \mbox{d} t \)
\( \mbox{P}_{gem} = \frac{1}{\mbox{T}} \, \int_0^T \mbox{U}(t) \mbox{I}(t) \, \mbox{d} t \)
\( \mbox{P}_{gem} = \frac{1}{\mbox{T}} \, \int_0^T \mbox{I}(t)} \mbox{R} \cdot \mbox{I}(t) \, \mbox{d} t \)
\( \mbox{P}_{gem} = \frac{1}{\mbox{T}} \, \int_0^T \{ \mbox{I}(t)} \}^2 \, \mbox{d} t \, \cdot \, \mbox{R} \)
\( \mbox{P}_{gem} = \left [ \{ \mbox{I}(t)} \}^2 \right ]_{gem} \, \cdot \, \mbox{R} \)
- ukster
- Artikelen: 0
- Berichten: 4.917
- Lid geworden op: za 28 nov 2015, 10:42
Re: maximaal vermogen
Dank voor jullie zeer gewaardeerde bijdrage(n) in dit topic.
Verschillende Inzichten delen is de kracht van dit Forum.
Verschillende Inzichten delen is de kracht van dit Forum.
- WillemB
- Artikelen: 0
- Berichten: 654
- Lid geworden op: do 20 feb 2014, 17:51
Re: maximaal vermogen
@ Puntje, dat klopt zo kan het ook, geeft het zelfde resultaat, elke formule voor berekening van P werkt.
Ik zit meer met de theorie en de praktijk, heb een test opstelling, met HP apparatuur, die echt true RMS kan meten.
Maar ook de mist ingaat met dit soort signalen.
Ik heb nu een test met een echte driehoeks spanning , om daar true RMS mee te meten, 1 V - 0 V echt een rechte lijn.
De gemiddelde waarde op U niveau is 500 mV maar de berekende true RMS is 578 mV.
Maar dat is moeilijker in de praktijk om dat goed te meten, zelfs met lab meetapp. die komt nog niet verder dan 540 mV.
Ik zit meer met de theorie en de praktijk, heb een test opstelling, met HP apparatuur, die echt true RMS kan meten.
Maar ook de mist ingaat met dit soort signalen.
Ik heb nu een test met een echte driehoeks spanning , om daar true RMS mee te meten, 1 V - 0 V echt een rechte lijn.
De gemiddelde waarde op U niveau is 500 mV maar de berekende true RMS is 578 mV.
Maar dat is moeilijker in de praktijk om dat goed te meten, zelfs met lab meetapp. die komt nog niet verder dan 540 mV.
Sinds de uitvinding van tijd, hebben we het niet meer, en kunnen we het ook niet meer vinden.
En wie haast heeft moet langzamer lopen.
En wie haast heeft moet langzamer lopen.
- Professor Puntje
- Artikelen: 0
- Berichten: 7.574
- Lid geworden op: vr 23 okt 2015, 23:02
Re: maximaal vermogen
Is je signaal wel een echte wisselspanning, dus met gemiddelde waarde nul?
- WillemB
- Artikelen: 0
- Berichten: 654
- Lid geworden op: do 20 feb 2014, 17:51
Re: maximaal vermogen
Nee juist niet, het is een zuivere driehoeks spanning, er zit geen enkele sinus in.
Ik heb een generator die elke gewenste golf vorm kan maken.
Maar dit is wel een bekend verschijnsel, het is heel moeilijk om wat in deze topic naar voren kwam
in de praktijk te meten, dit euvel doet zich ook voor bij de slimme meters. Power meten volgens
de gemeten gemiddelde van de kwadraten is een klus.
Slimme meters moeten ook volgens de formules werken die genoemd zijn, en de signalen
op het net door led en schakelende voedingen zijn niet meer sinus vormig maar heel grillig.
Maar voor mij is het een leuk praktijk testje en experiment.
Ik heb een generator die elke gewenste golf vorm kan maken.
Maar dit is wel een bekend verschijnsel, het is heel moeilijk om wat in deze topic naar voren kwam
in de praktijk te meten, dit euvel doet zich ook voor bij de slimme meters. Power meten volgens
de gemeten gemiddelde van de kwadraten is een klus.
Slimme meters moeten ook volgens de formules werken die genoemd zijn, en de signalen
op het net door led en schakelende voedingen zijn niet meer sinus vormig maar heel grillig.
Maar voor mij is het een leuk praktijk testje en experiment.
Sinds de uitvinding van tijd, hebben we het niet meer, en kunnen we het ook niet meer vinden.
En wie haast heeft moet langzamer lopen.
En wie haast heeft moet langzamer lopen.
- klazon
- Pluimdrager
- Artikelen: 0
- Berichten: 7.933
- Lid geworden op: ma 09 mei 2005, 23:52
Re: maximaal vermogen
Slimme meters werken niet met deze formules. Die samplen duizenden malen per seconde en vermenigvuldigen de samples van stroom en spanning.WillemB schreef: Slimme meters moeten ook volgens de formules werken die genoemd zijn, en de signalen
op het net door led en schakelende voedingen zijn niet meer sinus vormig maar heel grillig.
- Professor Puntje
- Artikelen: 0
- Berichten: 7.574
- Lid geworden op: vr 23 okt 2015, 23:02
Re: maximaal vermogen
@ WillemB
Het is mij nog niet duidelijk aan wat voor signaal je meet. Is dat zoiets als U1 of als U2?
Het is mij nog niet duidelijk aan wat voor signaal je meet. Is dat zoiets als U1 of als U2?
- WillemB
- Artikelen: 0
- Berichten: 654
- Lid geworden op: do 20 feb 2014, 17:51
Re: maximaal vermogen
@ Klazon, die samples worden door software verwerkt , volgens de som der kwadraten van het vermogen, dus
ik zie het verschil niet, het idee erachter is hetzelfde als de formules die hier gebruikt worden.
Het gaat er ten slotte om hoe je de theorie omzet in hardware en software.
Die software is nu in onderzoek of die het wel goed doet in sommige meters, want true RMS in niet voldoende.
En ook niet het vermenigvuldigen van stroom en spannings samples is te simpel, dan gaat het fout.
@ Puntje, de bovenste grafiek, en de opgaande flank is niet schuin maar recht, een rechthoekige driehoek.
ik zie het verschil niet, het idee erachter is hetzelfde als de formules die hier gebruikt worden.
Het gaat er ten slotte om hoe je de theorie omzet in hardware en software.
Die software is nu in onderzoek of die het wel goed doet in sommige meters, want true RMS in niet voldoende.
En ook niet het vermenigvuldigen van stroom en spannings samples is te simpel, dan gaat het fout.
@ Puntje, de bovenste grafiek, en de opgaande flank is niet schuin maar recht, een rechthoekige driehoek.
Sinds de uitvinding van tijd, hebben we het niet meer, en kunnen we het ook niet meer vinden.
En wie haast heeft moet langzamer lopen.
En wie haast heeft moet langzamer lopen.
- Professor Puntje
- Artikelen: 0
- Berichten: 7.574
- Lid geworden op: vr 23 okt 2015, 23:02
Re: maximaal vermogen
Dus zo?
-
EvilBro
- Artikelen: 0
- Berichten: 7.081
- Lid geworden op: vr 30 dec 2005, 09:45
Re: maximaal vermogen
WillemB lijkt te suggereren dat het voldoende is om te weten wat het ladingverschil is. Dit lijkt mij onjuist. Immers:Ik zal nog eens kijken of het dan toch ook via de door WillemB aangegeven weg kan, ik liep daarbij vast. Maar misschien zie je ook hoe dat dan moet.
\(E(0) = \frac{(Q(0))^2}{2 \cdot C}\)
\(E(T) = \frac{(Q(T))^2}{2 \cdot C}\)
\(\Delta E = \frac{(Q(0))^2 - (Q(T))^2}{2 \cdot C}\)
En dus:
\(P_{gem} = \frac{(Q(0))^2 - (Q(T))^2}{2 \cdot C \cdot T} = \frac{(Q(0) - Q(T)) \cdot (Q(0) + Q(T))}{2 \cdot C \cdot T}\)
\(= \frac{(\Delta Q) \cdot (\Delta Q + 2 \cdot Q(T))}{2 \cdot C \cdot T}\)
De eindlading van de condensator (Q(T)) kun je niet uitdrukken in het ladingverschil. Het is dus onmogelijk om deze te elimineren uit het proces en dus is alleen het ladingverschil niet voldoende om het gemiddelde vermogen te berekenen.Je zou natuurlijk wel een benadering kunnen doen als Q(T) veel kleiner is dan het ladingverschil:
\(P_{gem} \approx \frac{\Delta Q^2}{2 \cdot C \cdot T}\)
- Professor Puntje
- Artikelen: 0
- Berichten: 7.574
- Lid geworden op: vr 23 okt 2015, 23:02
Re: maximaal vermogen
@ EvilBro
Ah - bedankt. Ik had daar ook al grote twijfels bij, maar het is dus inderdaad onmogelijk.
Ah - bedankt. Ik had daar ook al grote twijfels bij, maar het is dus inderdaad onmogelijk.