4 van 5
Re: rapunzel
Geplaatst: di 11 dec 2018, 21:06
door ukster
even kort door de bocht, 14,23 slagen
Re: rapunzel
Geplaatst: di 11 dec 2018, 21:08
door Xilvo
Leuk! We weten in ieder geval al dat de diameter van de lier er niet toe doet!
Re: rapunzel
Geplaatst: di 11 dec 2018, 21:29
door CoenCo
Ik kwam op 19,6 radialen = 3,11 slagen?
Re: rapunzel
Geplaatst: di 11 dec 2018, 21:39
door ukster
ik ging van het verkeerde uit!(teveel door de bocht)
T2=T1.aantal slagen. e(μdβ)
500=10.aantal slagen. e(0,2*2π)
500=10 aantal slagen*(3,51358)
aantal slagen =500/(10*3,51358)=14,23
Het is natuurlijk 500=10.e(n.μd.β)
1,2566.n=ln(50)
n=3,11 :eusa_sick:
Re: rapunzel
Geplaatst: di 11 dec 2018, 22:47
door ukster
Ik zie hierin toch ook een relatie met fasedraaiing in het complexe vlak.
Hierbij komt Euler om de hoek kijken
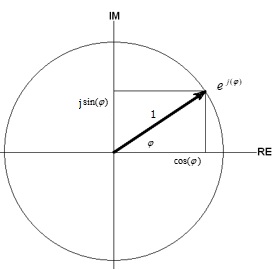
- fasedraaiing in het complexe vlak 969 keer bekeken
Re: rapunzel
Geplaatst: wo 12 dec 2018, 09:53
door Xilvo
Kan de afleiding niet simpeler?
Ook weer even 'kort door de bocht':
\(\varphi=\frac{\Delta x}{2.r} \)
\(\Delta F _ \perp = 2.\varphi.s=\frac{s.\Delta .x}{f}\)
\(\frac {\Delta F}{\Delta x}=\frac{s}{r}\)
\(\frac{ds}{dx}=\mu \frac{dF}{dx}=\mu \frac{s}{r}\)
met
\(dx=r.d\varphi\)
\(\frac{ds}{d\varphi}=\mu s\)
geeft
\(s=a.e^{\mu.\varphi}\)
Re: rapunzel
Geplaatst: wo 12 dec 2018, 11:52
door ukster
Ik heb twijfels.dit is geen afleiding voor de algemene situatie T2≠T1
Vanwege de symmetrie is wel voldaan aan de evenwichtsvoorwaarden :SIGMA: Fx=0 en :SIGMA: Fy=0
maar wrijving speelt nu geen rol.
ik neem aan dat in s=a.eμφ a=800N?
Re: rapunzel
Geplaatst: wo 12 dec 2018, 12:01
door Xilvo
Nee, dat klopt. Dit is weer voor het geval het touw op het randje van slippen staat, wegens
\(\frac{ds}{dx}=\mu \frac{dF}{dx}=\mu \frac{s}{r}\)
De wrijving is dus maximaal.
a=800 N volgt uit de randvoorwaarde als φ=0 gekozen wordt bij het verticale raakpunt van het touw.
N.B. De wrijvingskracht kan naar rechts of links gericht zijn; ook kun je φ linksom of rechtsom positief nemen.
Je kunt de μ in de e-macht dus altijd van een min-teken voorzien.
Re: rapunzel
Geplaatst: wo 12 dec 2018, 12:11
door ukster
?? Bij twee even grote krachten staat het touw toch niet op het randje van slippen?
Er is evenwicht en de wrijving is nul zou ik denken.
Re: rapunzel
Geplaatst: wo 12 dec 2018, 12:15
door Xilvo
Nee, de krachten zijn niet even groot. Je begint bij φ=0 met s=800 N, en s neemt dan toe of af met toenemende φ.
Daar komen dan precies dezelfde waardes uit als in jouw bericht #10 staan.
Re: rapunzel
Geplaatst: wo 12 dec 2018, 12:55
door ukster
Aha..
Re: rapunzel
Geplaatst: do 13 dec 2018, 15:16
door CoenCo
Volgende vraag:
De fabrikant van de lier, heeft een nieuw materiaal ontwikkeld, en wil daarvan de wrijvingscoefficient bepalen.
Gelukkig hebben ze een stagiar, en die gaat dat wel even doen... Hij heeft een plan opgesteld:
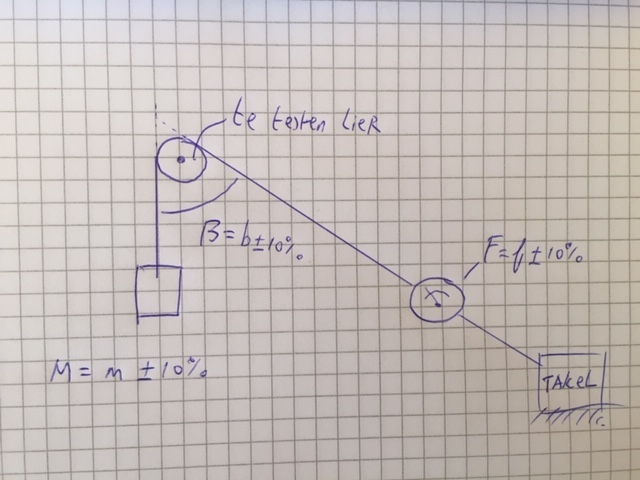
- IMG_2335 968 keer bekeken
Er wordt een gewicht opgehangen, touw over de lier, krachtsensor, takel.
Het plan is om te meten welke kracht er nodig is om het blok omhoog te trekken, en daaruit de wrijvingscoefficient te bepalen.
Het probleem met sommige stagiars is alleen dat ze nogal onnauwkeurig zijn, een meetfout van +/-10% is niet ongewoon. Als stagebegeleider heb je budget om 1 van de 3 parameters/meetinstrumenten door een professional te laten controleren: Massa testgewicht, hoek Beta of trekkracht.
De vraag aan de stagair: Welke parameter kan ik het beste laten controleren? Waarom? Toon aan met een berekening.
Re: rapunzel
Geplaatst: do 13 dec 2018, 15:19
door Xilvo
En μ is (exact) bekend?
Re: rapunzel
Geplaatst: do 13 dec 2018, 15:29
door CoenCo
mu is de parameter die gemeten/bepaald moest worden.
Re: rapunzel
Geplaatst: do 13 dec 2018, 15:35
door Xilvo
Ah, ja, natuurlijk.
Ik zal de volgende keer beter opletten

De hoek β zou ik professioneel laten vaststellen.