sciencetalk

Wat ik niet begrijp is dat er maar één oplossing voor de versnelling a is waarbij de blokjes in rust blijven, ik zou eerder een interval verwachten omdat de wrijvingsweerstand ook alle waarden uit het interval [-μN,+μN] kan aannemen. Kennelijk is er iets wat ik over het hoofd zie, en ik probeer er door de beschouwing van verschillende varianten achter te komen wat dat is.

ik zou eerder een interval verwachten omdat de wrijvingsweerstand ook alle waarden uit het interval [-μN,+μN] kan aannemen

Dat is wat CoenCo in het aangehaalde bericht stelt, en het klinkt zeer overtuigend.

Met zijn analyse:
- Er is wat mis met Interactive Physics
- Wij maken een denkfout, c.q. zien iets over het hoofd dat I.P. wel meeneemt

Ben ik het eens. Nu nog de correcte en overtuigende oplossing vinden.

Ik zal kijken of ik nog wat testjes kan doen.

interval concept!
voor μ=0,4 bedraagt de versnelling 2,943 m/s² (=0,3g) (wrijvingskracht naar links gericht)
voor μ=0 bedraagt de versnelling 4,905 m/s² (=0,5g)
Bij F_max is de versnelling zo groot dat de wrijvingskracht op m2 van richting omkeert.
a=(Fw+m1.g)/(m1+m1)=6,866 m/s² (=0,7g)
F_max=(m1+m1+m3)(a+Cr.g)=708,2N
Interval waarbij m2 niet zakt: 335,5N < F_karretje < 708,2N

Wat ik niet begrijp is dat er maar één oplossing voor de versnelling a is waarbij de blokjes in rust blijven

Morgen zal ik een uitgebreide simulatie maken van dat (

) karretje, met mooie ronde getallen (Mtotaal = 100 kg, g =10) waarbij ik de versnelling zal laten oplopen en op iedere relevante parameter een grafiekje zetten. Kunnen we zien hoe volgens I.P. het geheel zich gedraagt onder toename van F.

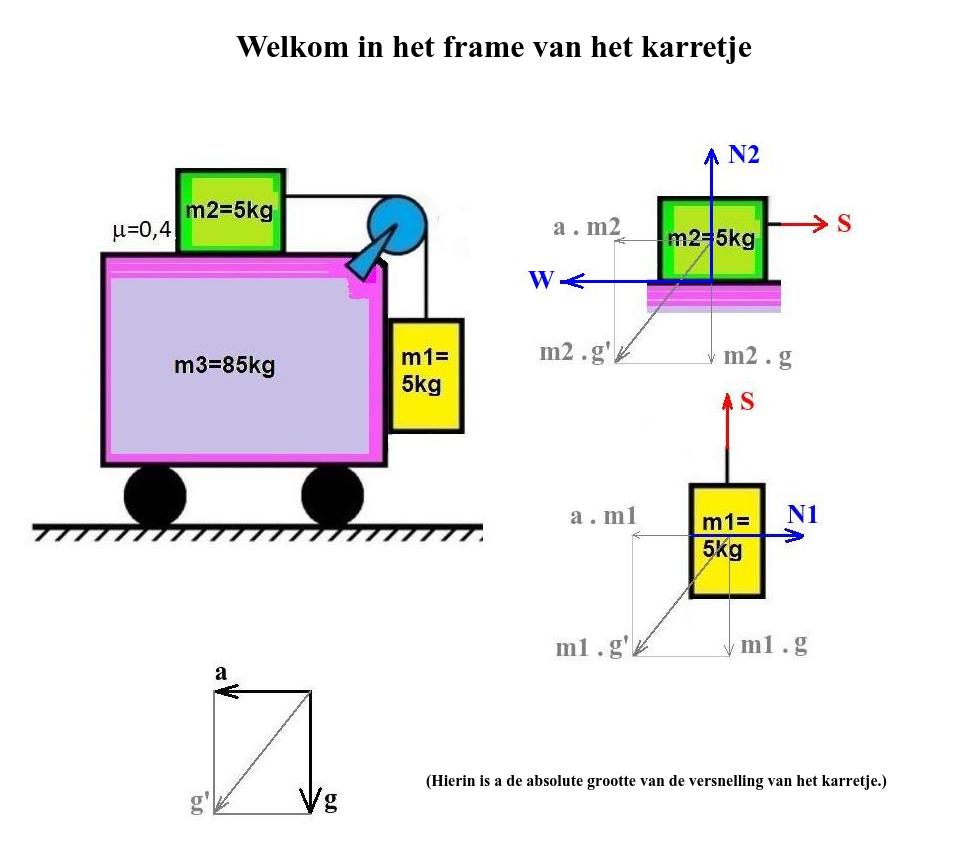
: karretje-frame 599 keer bekeken

Dit is de situatie in het frame van het karretje wanneer de blokjes ten opzichte van het karretje in rust zijn. We zien dat:

\( W + a \cdot \mbox{m}_2 = S \)

\( \mbox{m}_1 \mbox{g} = S \)

Zodat:

\( W + a \cdot \mbox{m}_2 = \mbox{m}_1 \mbox{g} \)

Omdat in ons geval m₁ = m₂ (die we verder m noemen) krijgen we:

\( W + a \cdot \mbox{m} = \mbox{m} \mbox{g} \)

We zien dat voor a = g geen wrijvingskracht W benodigd is om de blokjes in rust te houden, dat is dus een mogelijkheid. De twee uiterste waarden voor de wrijvingskracht zijn W+ = +μN₂ en W- = -μN₂. Wanneer de versnelling a onder g zakt moet de wrijvingsweerstand in de aangegeven richting bijspringen om de blokjes in rust te houden. Dus vinden we als minimale versnelling a_min waarbij de blokjes op het karretje nog net in rust blijven:

\( W^+ + a_{min} \cdot \mbox{m} = \mbox{m} \mbox{g} \)

\( \mu N_2 + a_{min} \cdot \mbox{m} = \mbox{m} \mbox{g} \)

\( \mu \mbox{m} \mbox{g} + a_{min} \cdot \mbox{m} = \mbox{m} \mbox{g} \)

\( \mu \mbox{g} + a_{min} = \mbox{g} \)

\( a_{min} = \mbox{g} - \mu \mbox{g} \)

\( a_{min} = (1 - \mu) \mbox{g} \)

Dat is ook het genoemde betoog van CoenCo, maar Interactive Physics denkt daar vooralsnog anders over (samen met Rik en -vooralsnog- ik).

Ik kan mijzelf toch moeilijk ongelijk geven zolang de fout in mijn bewijs niet is gevonden...

ukster schreef:
jawel,
da's toevallig!
a_min=(1-μ)g=(1-0,4)g=0,6g=0,6*9,81=5,886 m/s²
als je dit door 2 deelt krijg je a=2,943 m/s²
en dat is wat ik hieronder heb berekend met a=(m1.g - Fw)/(m1+m2) = 2,943 m/s²
a=m1(1-μ)g/(m1+m2)=(1-μ).g/2 het betreft immers de twee massa's samen. (volgt uit vergelijking 1+vergelijking2)
Stilstaand karretje.jpg

m1.g=49,05N
Fw=μ.N=μ.m2.g=19,62N

m1.g - S = m1.a

S - Fw = m2.a
versnelling a=(m1.g - Fw)/(m1+m2) = 2,943 m/s²
Spankracht S = Fw +m2.a = 34,335N

versnelling karretje: a=(F - Cr.(m1+m2+m3).g) / (m1+m2+m3) = 2,943 m/s²
F=(m1+m2+m3).(a+Cr.g) =(85+5+5).(2,943+0,06.9,81) = 335,5N

als m2 geen wrijving ondervindt (μ=0), dan a=4,905 m/s²

Spankracht S= 49,05N en de kracht op het karretje F=521,9N
Als er ook geen rolwrijving is dan F=465,98 N

@ ukster

Je schrijft:

m1.g - S = m1.a

S - Fw = m2.a

Maar die eerste vergelijking klopt niet! Het blokje m1 mag niet verticaal bewegen, dus mag er ook geen netto verticale kracht op werken.

oplossingsstrategie!

ukster schreef:
1. m1,m2 , μ en g bepalen de versnelling a=(m1.g - Fw)/(m1+m2)= (1-μ) .g/2 van het subsysteem. (karretje staat stil) (a<g)

2. Het hoofdsysteem F,(m1+m2+m3) moet dezelfde versnelling krijgen zodat hoofdsysteem en subsysteem ten opzicht van elkaar geen versnelling hebben. m1 zakt dan niet naar beneden. De benodigde minimale kracht op karretje: F_min =(m1+m2+m3).(a+Cr.g)

Strategie of niet - zolang er een netto verticale kracht op m1 werkt zal het blokje in verticale richting in beweging komen. En die netto verticale kracht op m1 is volgens mij S - m1.g . Dat moet dus nul zijn, in tegenstelling tot je eerste vergelijking. In je plaatje staat ook een neerwaartse versnelling a die in die richting niet bestaat.

voor het stilstaand karretje is de versnelling van m1 wel degelijk neerwaarts. a=(m1.g - Fw)/(m1+m2) = 2,943 m/s²

ukster schreef: voor het stilstaand karretje is de versnelling van m1 wel degelijk neerwaarts.

En dus?

vervolgens geven we het karretje precies dezelfde versnelling, waardoor de relatieve versnelling ten opzichte van elkaar wegvalt (a=0) en dus m1 niet daalt.

Omdat het blokje bij stilstand van het karretje een verticale versnelling a krijgt geven we het karretje een zelfde horizontale versnelling a waardoor de verticale versnelling van het blokje wegvalt? Je moet er maar opkomen! Ik zie geen enkele reden waarom je zo de (minimale) versnelling van het karretje zou vinden waarbij de blokjes nog net in rust blijven.

Maar los daarvan klopt je eerste vergelijking ook gewoon niet wat je eenvoudig aan de hand van verticaal krachtenevenwicht voor m1 kunt vaststellen.

sciencetalk

karretje

Re: karretje

Re: karretje

Re: karretje

Re: karretje

Re: karretje

Re: karretje

Re: karretje

Re: karretje

Re: karretje

Re: karretje

Re: karretje

Re: karretje

Re: karretje

Re: karretje

Re: karretje