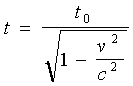sciencetalk

Als ik lengtecontractie goed begrijp dan vindt dat alleen plaats in de richting van de beweging? of wat?

Dus als een ladder(om in de sferen te blijven) gaat bewegen met relativitsiche snelhden , en wel zo dat hij recht gaat, (dus niet diagonaal maar gewoon met een zo kleinmogelijk frontaal oppervlakte) dan word de trap alleen minder lang, en niet minder breed, toch?

De contractie treedt op in de bewegingsrichting.

Nu ik heb ook een vraag over lengte contractie en ik dacht ik zal ze hier maar bijzetten.

Deze lengetcontractie, treedt deze werkelijk op, of is dit een illusie voor de waarnemer?

Nu ik stel mij een plaats voor buiten het heelal voor, zonder ruimte en zonder tijd. Stel je bevindt je hierin en daar is een soort overzicht van het heelal, met de exacte plaats van elk deeltje, dus je weet de exacte plaats en toestand van alles, zonder dat dar tijd voor nodig is. Zou deze waarnemer in deze theoretische plaats ook zien dat deze lengtecontractie optreedt of helemaal niets, dat het voorwerp gewoon even lang blijft en het een illusie is? Theoretisch allemaal dan hé.

Hij zal de contractie zien. Ook zal hij meten dat het ruimteschip zwaarder is. Je krijgt alleen de eigenlengte als je stilstaat relatief tot het voorwerp.

Er is een minicursus waarin dat perfect staat uitgelegd

Maar ik heb iets vreemds bedacht

hoor aan.

We nemen een paradox met een trein . voor de duidelijkheid een plaatje(uit de minicursus)



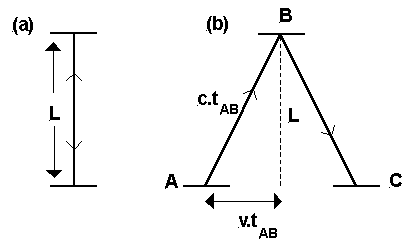
Dit is wat er gebeurt. Een meisje in een trein, heeft op de vloer een lamp nergezet en aan het plafond een spiegel zodat het licht dat de spiegel raakt word weerkaatst. weer terug naar de bron.

Er staat ook nog een jongen te kijken als waarnemen van buiten de trein.

Nu zet het meisje de lamp aan en het licht gaat voorhaar recht omhoog en daarna weer naar beneden, en komt weer terecht waar het vandaan kwam,(die links van het plaatje). terwijl het meisje dat deed, kwam de langs de jongen, en voor de jongen gaat de lichtbundel niet alleen omhoog en omlaag maar ook van rechts naar links, (die rechterplaatje)

nu het volgende. De afstanden waar over word gesproken:

ik kijk alleen naar de afstand van de lamp tot het plafond. in het plaatje dus "L" genaamd.

Je kan de afstand L bereken met de volgende formule S=v*t

voor een lichtbundel in deze situatie geldt :L=c*t

omdat de trein met hoge snelheden beweegd heeft het meisje een andere tijd dan de jongen, dus schrijf ik het zo. L=c*t_meisje

en voor de jongen geld:L=c*t_jongen

en aangezien het meisje minder tijd verbruikt, krijg je dat haar L kleiner wordt, en zo niet alleen een contractie optreedt in de bewegingsrichting maar ook in de hoogte, ze kan de lamp natuurlijk ook plat leggen, en zo ontstaat er in de breedte ook nog contractie, en zo ontstaat er ruimte contractie,

ruimte=lengte*hoogte*breedte

aangezien ik hier nooit van heb gehoord, en het me sterk lijkt dat ik met iets revolutionairs komt, vraag ik me af, waar zit mijn fout?

of je vindt het natuurlijk een goed idee, dan hoor ik dat nog liever.

Er verandert niets aan de tijd van de jongen ten opzichte van het meisje, want y = y'. Alleen over de x-as transformeert de tijd.

Alleen over de x-as transformeert de tijd.  

tijdt is toch geen vector? die je een richting kunt geven?

tijd is toch iets wat in jou stelsel plaats vindt?

Antoon,

De lengte die het licht in het stelsel van het meisje aflegt is L. Echter in het stelsel van de jongen is dit de schuine zijde van de driehoek en dus niet L.

Ah, maar dan zit ik wel met een probleem, stel ik wil de verhouding van de tijd berekenen. dus dat ik zo'n dergelijke formule krijg:



Omdat t=S/v geldt, en de snelheid c is, en de t niet voor het jongen en meisje gelijk is, moet de S verschillen, dat zie je ook in het plaatje.

dus ik hoef alleen maar de verhouding tussen de S_jongen en de S_meisje. het is makkelijker om alleen maar de eerste helft te doen, dus totdat het enkel het dak raakt.

de formule voor de verhouding van tijden is:

t_meisje/t_jongen=S_meisje/S_jongen

de S van het meisje is gewoon c*t. en de S van de jongen is met behulp van pytagoras: (L²+a²)

a is de afstand die de trein aflegd terwijl het licht onderweg is naar het plafond.

dus

t_meisje/t_jongen=c*t/ (L²+a²)

a=v*t

en L=?welke waarde moet ik voor L nemen?voor het meisje is het c*t

maar wat is het dan voor de jongen?

als het dezelfde hoogte heeft, dan kun je het ook berekenen met c*t. maar omdat je het voor hem moet zijn , krijg je een andere t, zo bedacht ik het. om moet je dan voor de jongen de t van het meisje invullen om de hoogte te berekenen? dan gebeurt er ook iets vreemd, want dan word te trein voor de jongen steeds minderhoog,(toch?)

dus dan klopt het in 2 situaties niet.

Als de jongen de zelfde lengte heeft als het meisje, en het meisje heeft als L=c*t_meisje en omdat het t_meisje steeds verder afwijkt van de tijd van de jongen, gaat voor de jongen de trein er lager uitzien.

en als ieder zijn eigen t in moet vullen, dan klopt het ook niet meer.

ik weet dat ik soms heel dwars kan doen, maar toch zou ik graag iemand willen hebben die het me duidelijk uitlegt

t_meisje/t_jongen=c*t/ (L²+a²)

vanwaar die gewone t? ofwel is het de tijd van het meisje ofwel die van de jongen!

L= c*t_meisje

a=v*t_jongen

invullen en uitwerken.

peterdevis schreef:t_meisje/t_jongen=c*t/ (L²+a²)

vanwaar die gewone t? ofwel is het de tijd van het meisje ofwel die van de jongen!

L= c*t_meisje

a=v*t_jongen

invullen en uitwerken.

die die gewone t is van het meisje.

maar jung, als L=c*t_meisje

dan gaat er toch iets fout. let op:

De tijd van de jongen is anders dan de tijd van het meisje, dus de jongen ziet dan een kleinere trein voorbij razen.als hij dezelfde L heeft als het meisje.

want als de trein stilstaat is er geen verschil in tijd verstrek, maar zodra hij gaat rijden wel, een aangezien L=c*t_meisje en de 2 t's lopen niet meer gelijk dan gaat het kleiner worden voor de jongen

Ik zal mijn standpunt (wat het is geworden) even duidelijk opschrijven.

Ik denk dat er naast tijdsdilatie en massa vermeerdering, en lengtecontractie , er ook iets bestaat als Ruimte contractie.

Dat zal ik proberen te onderbouwen, teneerste moet het verhaal van de trein kennen.

De trein heeft een bepaalde hoogte, die kun je opmeten met een meetlat maar ook berekenen ,als je weet hoeland het licht erover doet om tot het plafond te komen, dan weet je hoe hoog de trein in.

Want L=c*t

Ten eerste is de t voor de jongen en het meisje niet gelijk, dus zou je zeggen dat daar als contratie plaatsvindt. ben je het met Peter eens, over dat de jongen niet mag zeggen L=c*t omdat zijn licht bundel een andere weg aflegd, dan kun je vinden dat hij net als het meisje, de t in moet vullen die het meisje in haar trein meet.

We nemen 2 gelijkte treinen. waarin als je met de zelfde snelheid reist ze dus ook dezelfde hoogte hebben, daar ben ik het zelfd mee eens.

maar nu gaat alleen de trein met het meisje erin rijden, en die meet L=c*t

en de jongen doet ook voor heb L=c*t ze krijgen beide dezelfde L eruit.

maar omdat voor de jongen de tijd van het meisje slomer gaat dan zijn eigen tijd. nu heeft het meisje problemen met formule's in vullen, en ze hebben een manier gevonden om te communiceren, zodat de jongen de berekeningen kan maken voor het meisje, omdat voor de jongen de tijd van het meisje slomer gaat dan die van hem en visaversa, kan zei dus meer doen in de tijd dat de jongen het kan, dus als zei dan doorgeeft met een sinjaal "start" en "geraakt" en daartussen ging het licht van beneden naar boven, dan krijgt hij een andere tijd door ,een tijd die kleiner is dan zijn eigen gemeten tijd voor zijn wagon, dus ziet hij de trein van het meisje kleiner dan de trein van zichzelf(die stilstaat)

nou,ik heb langer dan een dag gewacht,en dat is lang voor het forum deze tijd, maar geen verdere reacties.

Ik hoor graag wat mensen er van denken ook al hebben ze geen achtergrond praat voor hun standpunt.

verder draagt het niet bij aan de discussie maar ik hoor graag:"ik ben het er mee eens"

Ze zullen dezelfde L meten, want het licht legt, zoals de jongen het ziet meer afstand af (het licht beweegt schuin). Dat verrekend met de tijddilatatie, kom je op hetzelfde uit.

Ze zullen dezelfde L meten, want het licht legt, zoals de jongen het ziet meer afstand af (het licht beweegt schuin). Dat verrekend met de tijddilatatie, kom je op hetzelfde uit.

volgens mij heb je mijn laatste post niet gevolgd.

De jongen zit nu ook in een trein die stil staat. en ze doen beide de proef waar ze de tijd meten, en dat vullen ze in in de formule L=c*t

Maar nu moet moet je jongen voor het meisje de t invullen, het meisje zegt start en stop, als de jongen dit hoort, dan gaat dit sneller voor het meisje ten opzichte van de jongen, dus als de jongen het dan invult krijgt hij een kleinere L eruit, terwijl als het meisje haar eigen t invult krijgt ze een dezelfde L eruit (daar ben ik het natuurlijk mee eens)ik zal het eens een keer proberen uit te werken na mijn werk