1 van 2
E-modulus
Geplaatst: vr 07 jan 2011, 16:17
door jmigchelbrink
Beste mensen,
Ik heb een vraag over het bepalen van het materiaal met een mechanicaschema.
De bekende gegevens zijn de aangebrachte belasting, 5N / 7,5N en 10N.
Ook is de doorbuiging in een bepaald punt bekend.
Verder is de constructie ingeklemd en met een rol ondersteund.
Onderstaande foto brengt hopelijk wat verduidelijking:

Punt A is de inklemming. Punt B is de roloplegging.
De hoekverdraaiing in punt A is 0. Verder is fi-b-links gelijk aan fi-b-rechts.
De constructie is statisch onbepaald en dus niet met de hand op te lossen. Nu schijnt het mogelijk te zijn met een vergeetmenietje en de toepassing van xEI in de noemer. Al weet ik niet meer precies hoe dat ging.
Heeft iemand tips? Ik wil dus uiteindelijk op E uitkomen. I is bekend, de afmetingen van het profiel zijn gegeven: 6,5mm breed en 40,4mm hoog.
Re: E-modulus
Geplaatst: vr 07 jan 2011, 16:44
door oktagon
Uit mijn leerboek Romijn Horseling:
Het verdraaien van de scharnierende oplegging is niet van invloed op de uitkomsten,doch veroorzaakt wel een inklemmingsmoment ( F*116/2)dat de grootte heeft van de helft van het koppel dat de draaiing veroorzaakt (F*116);mogelijk kun je hier wat mee beginnen of je zult even aan het Crossen moeten gaan.
Je kunt de verticale optredende reactie kracht bepalen en de D-en M-lijn opzetten en nmm. kun je de formule f=M*l^2/8EI toepassen,wel rekening houden met in welk gebied je zit.
Re: E-modulus
Geplaatst: vr 07 jan 2011, 19:28
door jmigchelbrink
Bedankt voor de tips! Middels het halve koppel zijn in ieder geval de reacties bekend.
Ma is 290 Nmm, FyA komt uit op 1,77N en FyB op 6,77N.
Dit geeft een Mmax boven het steunpunt van 580Nmm, en een moment tpv het meetpunt van 416,23Nmm.
Toch twijfel ik aan het vergeetmenietje wat ik moet gebruiken. Via jouw website heb ik de de lijst met doorbuigingsformules gedownload, hierin vind ik de situatie bij 12 nog het meest van toepassing. Desondanks zit daar in A een roloplegging ipv een inklemming..
De formule voor f1 zou dan 3^0.5/27 * ML^2/EI zijn.. Als ik deze toe pas kom ik op EI = 3,23 * 10^6.
Gedeeld door de I geeft dat een E-modulus van 3493,5.
Het gaat in dit geval om betonplex, dus een E van 8355 N/mm^2.. Ergens gaat het dus mis, is dit vergeetmenietje wel de goede?
Re: E-modulus
Geplaatst: vr 07 jan 2011, 22:59
door oktagon
Vergis jij je niet in de eenheden,controleer dat in je berekeningen;ik maak van de I : 35717 mm4,de rest nam ik vlug onder de loupe!
Ik krijg ook een onduidelijk antwoord,de E van hout varieert van 5000-10000 N/mm2,dus mogelijk is er een andere materie aan de orde (pu , pvc?)of is de betonplex een gegeven?
Re: E-modulus
Geplaatst: za 08 jan 2011, 07:41
door oktagon
Een andere benadering:
Bereken de optredende spanning
\(\sigma\)
veroorzaakt door het optredende moment van 416 Nmm ;je kunt de W berekenen.
Dan berekenen je (bij benadering) de verlenging in het deel van 93 mm en doorbuiging van 0.76 mm omdat hier een vrije verplaatsing is op het scharnier,er wordt een driehoek gevormd,waarvan je de schuine zijde kunt berekenen.
Theoretisch is dat een boogvorm,die echter de maat van de schuine zijde benadert ; er wordt hier veel benaderd met dit soort berekeningen.

Het verschil tussen de schuine zijde en de 93 mm is de verlenging over dat balkdeel,die is te beschouwen als de cosec (1/cosinus) van de hellingshoek H.
De benadering hiervan: sin H=0.76/93 =...... ,hieruit H en cosec H=...;een waarde >1;die waarde verminder je met 1 en je hebt de relatieve verlenging
\(\epsilon\)
en
\(\epsilon = \sigma\)
/
E ;dus daar rolt de
E uit.
Ik berekende geen uitkomst voor je,alleen de
\(\sigma\)
= 416/1738 N/mm2 (heel lege waarde );mag jezelf doen!
Volgens mijn uitkomst geeft dit een realistischer waarde aan.
Re: E-modulus
Geplaatst: za 08 jan 2011, 21:03
door jhnbk
Bepaal één symbolische formule voor de zakking in functie van de afmetingen, E, I en F. Je hebt dan enkel E als onbekende aangezien de zakking gekend is.
Re: E-modulus
Geplaatst: za 08 jan 2011, 23:30
door robertus58a
Met de volgende reactiekrachten en momenten:
\(F_{ya}=\frac{29}{82}F,\ \ \ F_{yb}=1\frac{29}{82}F \ en\ \ M_a=58F\)
kan je de zakking in h=genoemde punt (93 mm links van roloplegging B) eenvoudig berekenen aan de hand van volgend schema:
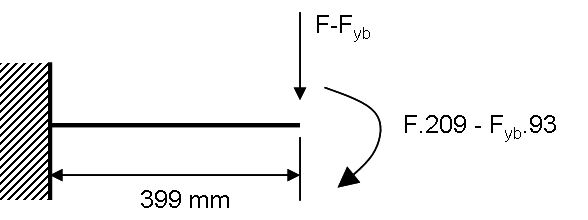
- Picture1 1595 keer bekeken
\(\frac{(F-F_{yb}).399^3}{3EI}+\frac{(F.209-F_{yb}.93).399^2}{2EI}=f\)
, of
\(-\frac{29}{82}.F.\frac{399^3}{3EI}+83\frac{9}{82}.F.\frac{399^2}{2EI}=f\)
, waaruit:
\(EI=-5\frac{79}{164}.399^2.\frac{F}{f}\)
(negatief teken: zakking omhoog), met I =
\(\frac{1}{12}40.4 *6.5^3 \ = \ 924.571mm^4\)
,
Voor de drie metingen is E dan: F/f : (5/0.76) E=6210 (7.5/1.12) E=6321 (10/1.47) E=6421.
Dit resultaat is nog steeds niet gelijk aan 8355 maar is in ieder geval in de buurt
Re: E-modulus
Geplaatst: zo 09 jan 2011, 14:20
door oktagon
@Robertus:
Mijn antwoord via de driehoek leverde E=7156 N/mm2 op!
@Jhnbk: Geef eens een aanzet tot die gedachte "symbolische" formule,ik paste een boekformule toe,maar die werkte niet,wrs. was die bedoeld voor een ligger op 2 steunpunten als benaderingsformule en ik meende die te kunnen gebruiken voor onderhavig geval.
Mogelijk is mijn gebruikte formule f=M*L^2/8EI te transformeren,door de veroorzaakte doorbuiging ter plekke van 93 cm van de rol door het inklemmingsmoment in de dan symbolische formule op te nemen;in mijn diverse literatuur kan ik er niets over vinden,mogelijk via een Integraal-berekening,maar dat is niet mijn sterkste kant van wiskundig denken en weten.

Na nog eens zoeken in mijn engelse leerboek van Duncan (appl.mechanics) zag ik een berekeningsmethode,die een ingeklemde ligger terugvoerde naar een ligger op 2 steunpunten,waarbij de inklemmingsmomenten van beide steunpunten als een continue gelijk moment en dus als tegenkracht werkend werd verwerkt in de formule welke geldt voor de ligger op twee stp.
Re: E-modulus
Geplaatst: zo 09 jan 2011, 15:05
door oktagon
Met hier nog de bijbehorende rest,die systeemtechnisch niet meer werd geaccepteerd:
De uitkomst deelt hij door EI;gehele verhaal wordt uitvoerig verklaard en resulteert bij een 2-zijdige ingeklemde ligger met 1 puntlast in het midden tot de formule f (doorbuiging)= PL3 / 192 EI. (basis: f=PL3 /48EI) Hier zit een vermenigv.factor 4 in.
Bij een gelijkm.belasting (q/m)bij een gelijksoortige ligger geeft dat f=qL4 /384 EI . (basis f=5 qL4/ 384EI ofwel 5ML2/48EI) Hier een verm.factor 5 !
Je ziet dat bovenstaand formules in een ?-verhouding staan met die van een ligger op twee steunpunten en dat hier dus mogelijk de ?-symboliek van Jhnbk zou kunnen worden verwerkt.
Re: E-modulus
Geplaatst: zo 09 jan 2011, 15:54
door oktagon
Mogelijk moet je van het systeem van een ligger op 2 steunpunten naar het systeem van een ligger op een 1z-inklemming en een rol uitgaan van een rechtlijnig verlopend inklemmingsmoment van 416N/2 over 492 mm verlopend naar 0.
Re: E-modulus
Geplaatst: zo 09 jan 2011, 17:57
door robertus58a
@Jhnbk: Geef eens een aanzet tot die gedachte "symbolische" formule,ik paste een boekformule toe,maar die werkte niet,wrs. was die bedoeld voor een ligger op 2 steunpunten als benaderingsformule en ik meende die te kunnen gebruiken voor onderhavig geval.
Wellicht ben ik niet geheel mee maar ik neem aan dat hetgeen ik eerder voorstelde -af te leiden via standaard vergeetmijnietjes- de"symbolische formule" is waar Jhnbk het over heeft.
Ik begrijp niet goed waarom dit belastingsgeval benaderd moet worden via bestaande belastingsgevallen die niet volledig representatief zijn voor deze situatie. Dit is m.i. eenvoudig te berekenen mbv de standaard vergeetmijnietjes (122368)
Re: E-modulus
Geplaatst: zo 09 jan 2011, 18:54
door oktagon
@Robertus,je citaat:
Ik begrijp niet goed waarom dit belastingsgeval benaderd moet worden via bestaande belastingsgevallen die niet volledig representatief zijn voor deze situatie. Dit is m.i. eenvoudig te berekenen mbv de standaard vergeetmijnietjes (122368)
Welke standaard vergeetmenietjes (122368) kunnen dus wel gebruikt worden;ik zie zo geen formules voor dit geval.
Niet standaardgevallen zoals ik liet zien werden afgeleid uit standaard gevallen en het onderwerp hier is een niet-standaardgeval.
Re: E-modulus
Geplaatst: zo 09 jan 2011, 19:32
door jhnbk
Wellicht ben ik niet geheel mee maar ik neem aan dat hetgeen ik eerder voorstelde -af te leiden via standaard vergeetmijnietjes- de"symbolische formule" is waar Jhnbk het over heeft.
Klopt. Ik heb zelf even geen tijd om hiernaar te kijken. Misschien morgen.
Re: E-modulus
Geplaatst: zo 09 jan 2011, 19:52
door jmigchelbrink
Wat een reacties! Alles even globaal doorgelezen, ga ik zeker me aan de slag morgen! Bruikbare tips, top :]
Re: E-modulus
Geplaatst: vr 28 jan 2011, 15:27
door jmigchelbrink
oktagon schreef:Een andere benadering:
Bereken de optredende spanning
\(\sigma\)
veroorzaakt door het optredende moment van 416 Nmm ;je kunt de W berekenen.
Dan berekenen je (bij benadering) de verlenging in het deel van 93 mm en doorbuiging van 0.76 mm omdat hier een vrije verplaatsing is op het scharnier,er wordt een driehoek gevormd,waarvan je de schuine zijde kunt berekenen.
Theoretisch is dat een boogvorm,die echter de maat van de schuine zijde benadert ; er wordt hier veel benaderd met dit soort berekeningen.

Het verschil tussen de schuine zijde en de 93 mm is de verlenging over dat balkdeel,die is te beschouwen als de cosec (1/cosinus) van de hellingshoek H.
De benadering hiervan: sin H=0.76/93 =...... ,hieruit H en cosec H=...;een waarde >1;die waarde verminder je met 1 en je hebt de relatieve verlenging
\(\epsilon\)
en
\(\epsilon = \sigma\)
/
E ;dus daar rolt de
E uit.
Ik berekende geen uitkomst voor je,alleen de
\(\sigma\)
= 416/1738 N/mm2 (heel lege waarde );mag jezelf doen!
Volgens mijn uitkomst geeft dit een realistischer waarde aan.
We zijn een heel eind gekomen met de benaderingsformules voor de hoekverdraaiing. Deze is inderdaad aan te nemen door de lijn als lineair te zien, en zo komen we redelijk in de buurt van de gezochte E-modulus.
Verder wilden we nog een controleberekening uitvoeren dmv de relatieve rek in dit deel van de ligger. Hoe kom je in dit geval op de waarde 1738 voor de spanning? Met M*e / I kom ik op een heel andere waarde.
Groetjes, Jochem

