1 van 1
Driespant
Geplaatst: wo 18 jan 2012, 00:34
door In physics I trust
Hoi,
In de afbeelding in bijlage zie ik niet hoe ik de globale evenwichtsvergelijkingen moet opstellen:
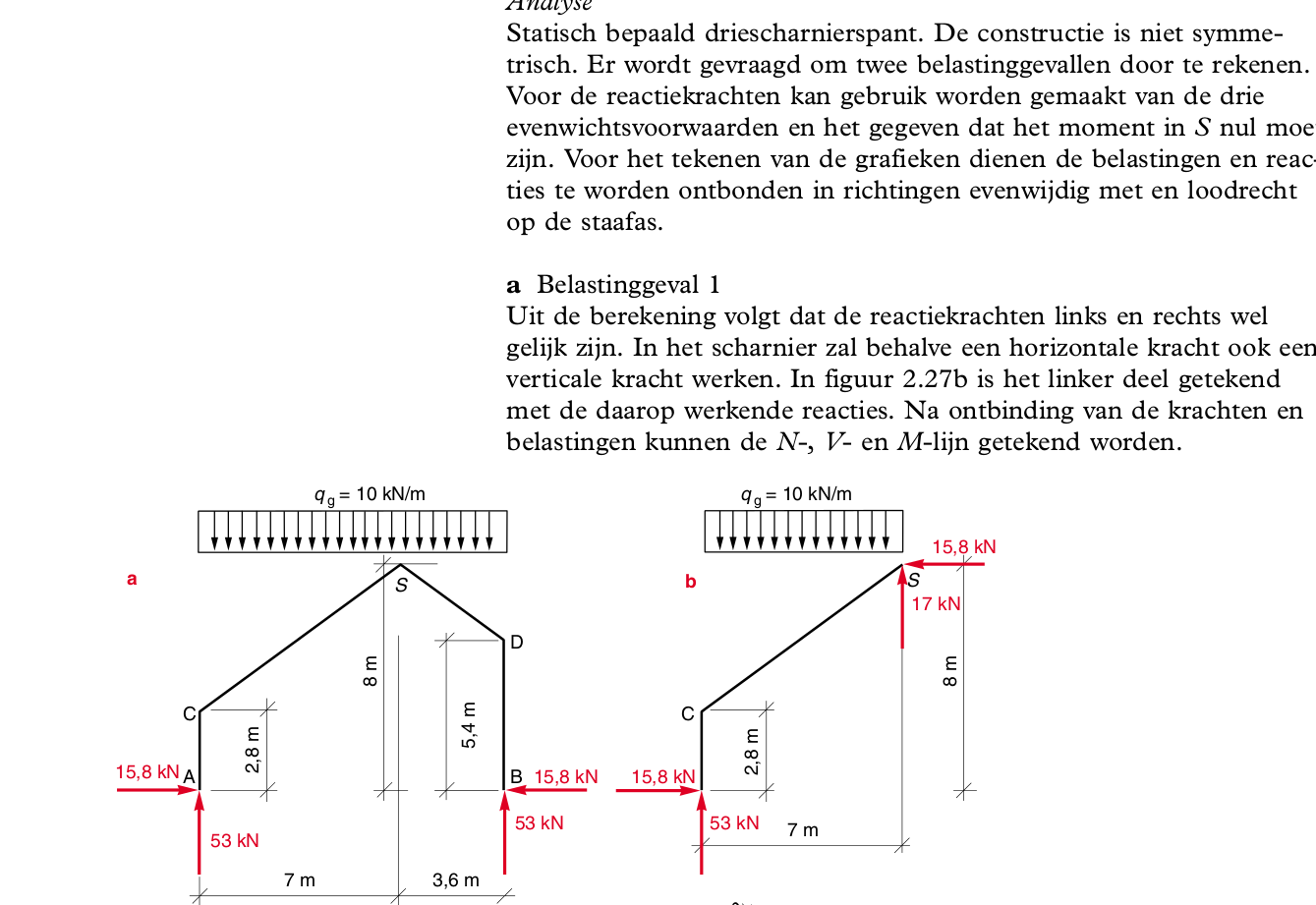
- plasme6 539 keer bekeken
Beschouw ik dit als twee keer een scharnier in A en B; aangevuld met een inwendig scharnier in S?
En hoe komt men aan die horizontale reactiecomponenten? Ik dacht eraan om die lopende belasting te projecteren volgens x- en y-richting, waarbij de horizontale reactiekracht dan de volgende is:
\(q(sin C * 7m - sin D * 3.6m )\)
Waarbij de hoeken genomen worden in de evident te beschouwen driehoeken (dus hoek van de schuine spanten met horizontale). Dan kom ik achter op 20.66 kN. Wat doe ik verkeerd?
Alvast bedankt!
Re: Driespant
Geplaatst: wo 18 jan 2012, 13:56
door dirkwb
Ik snap je vraag niet helemaal, zo zou ik het doen: som momenten om A is nul geeft de verticale reactiekracht in B. Dan som van krachten verticaal is nul geeft de verticale reactiekracht in A. Som van krachten horizontaal is nul geeft dan H_A = -H_B en som van moment om punt S is nul geeft de waardes van H_A en H_B.
Re: Driespant
Geplaatst: wo 18 jan 2012, 19:24
door jhnbk
Je hebt vier onbekenden: 2 per steunpunt (A en B)
Je hebt vier vergelijkingen: 3 evenwichtsvergelijkingen en ... ?
Dus kan je gewoon een stelsel uitschrijven
Re: Driespant
Geplaatst: vr 20 jan 2012, 23:36
door In physics I trust
Hoe breng ik de verdeelde belasting in rekening bij het momentenevenwicht, of eerder: wat is de arm van het moment van de 106 kN?
Re: Driespant
Geplaatst: za 21 jan 2012, 09:35
door jhnbk
Gewoon het midden van de belasting. Het is gelijkmatig verdeeld en heeft enkel een verticale component. Geraak je er voor de rest uit?
Re: Driespant
Geplaatst: za 21 jan 2012, 11:15
door In physics I trust
\(V_A*7m-H_A*8m+H_B*8m-V_B*3.6m=0Nm\)
Dat is de vierde vergelijking (moment in S=0)?
Re: Driespant
Geplaatst: za 21 jan 2012, 11:24
door jhnbk
Het buigmoment moet nul zijn. Je krijgt dus (afhankelijk van de tekenconventie maar ik denk dat ik nu dezelfde als jou gebruik)
0 + 7 HA = 8 HB + 10 7²/2
Re: Driespant
Geplaatst: za 21 jan 2012, 11:35
door In physics I trust
7 HA? Hoezo? Je neemt toch de afstand loodrecht op de krachtwerking? Dus horizontale kracht vermenigvuldigen met verticale afstand tot S; en verticale krachten vermenigvuldigen met de horizontale afstand?
Re: Driespant
Geplaatst: za 21 jan 2012, 12:14
door jhnbk
Oei oei, wat schreef ik daar allemaal

. Correctie :
0 + 7 V
A = 8 H
A + 10 7²/2
Re: Driespant
Geplaatst: za 21 jan 2012, 13:08
door In physics I trust
Inderdaad, vreemd dat ik het niet eerder doorhad. Bedankt voor je hulp!