1 van 2
Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 14:28
door Basicnerd
Hey,
Bij wiskunde D gaf iemand een raadsel waarvan zij beweerde dat hij oplosbaar was. Bekijk de bijlage en los het op als volgt:
Trek een lijn van A naar B
Trek een lijn van C naar D
De lijnen mogen elkaar niet kruisen
Je mag niet door een blok heen ( maar volgens mij kan je het raadsel ook niet oplossen als de blokken er niet zaten.)
Ik denk dat het niet kan, maar omdat ze maar blijven volhouden...
Bijlage:
https://docs.google.com/leaf?id=0B-WOiPYO8C...Nj&hl=en_US
Ik heb het al meerdere keren geprobeerd maar tot nu zonder resultaat.
Re: Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 14:40
door klazon
Hebben ze er bij gezegd dat de lijnen recht moeten zijn?
Re: Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 14:41
door Basicnerd
Hebben ze er bij gezegd dat de lijnen recht moeten zijn?
Nee, dat is niet gezegd. Ze mogen kronkelen, bochten maken, zolang ze elkaar maar niet kruisen.
Re: Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 14:44
door TD
Je bedoelt wellicht 'niet snijden'. Nee, dat is niet mogelijk (als je niet 'achter' zo'n letter heen kan, hetgeen uit de figuur onmogelijk blijkt; ik veronderstel ook dat je niet over zwarte randen mag). Je inschatting dat die blokjes in het midden er niet toe doen, is ook juist. Als die er niet staan, kan het nog steeds niet.
Re: Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 14:48
door Uomo Universale
Op de afbeelding die ik zie bestaat het 'veld' ook als een witte rand die rondom het buitenste vierkant van zwarte lijnen loopt. Als je dus één van beide lijnen (een lijn kan ook een kromme zijn) langs deze weg laat lopen, en de andere binnenin het vierkant bestaande uit de zwarte lijnen, dan ben je er.
Re: Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 14:49
door Drieske
Het gaat dus over deze figuur:
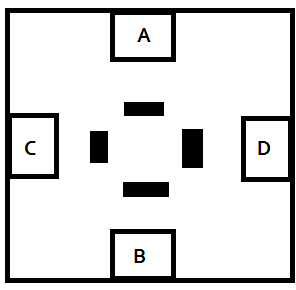
- raadsel 8573 keer bekeken
Probeer je de volgende keer zelf om je afbeelding rechtstreeks op het forum te uploaden? Dat is makkelijker voor degenen die willen helpen, en heeft als bijkomend voordeel dat de afbeelding niet weg is over een maand (bijvoorbeeld). Overigens verplaats ik dit ook naar Wiskunde.
Dan om op je vraag te antwoorden: neen, het is inderdaad niet mogelijk (en de blokjes doen er daarbij inderdaad niet zo toe). Zeker dat dit de (exacte) opgave is?
-edit- wat TD dus zei

.
Re: Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 14:50
door TD
Op de afbeelding die ik zie bestaat het 'veld' ook als een witte rand die rondom het buitenste vierkant van zwarte lijnen loopt. Als je dus één van beide lijnen (een lijn kan ook een kromme zijn) langs deze weg laat lopen, en de andere binnenin het vierkant bestaande uit de zwarte lijnen, dan ben je er.
Tja, het is maar de vraag of dat een bewust onderdeel van het raadsel is, of gewoon een restant van de schets. Ik vermoed dat je binnen de 'rand' moet blijven, maar daar is niets over gezegd.
Re: Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 14:58
door hanzwan
Dit gaat inderdaad niet , tenzij je door D of C mag wanneer je je lijn van A naar B trekt. Dit wordt nergens expliciet vermeld. Daarom zou ik van A naar B gaan door D heen zodat C nog steeds naar D kan.
Maar dat heeft dan weer weinig met wiskunde te maken en is meer een instinker.
Re: Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 15:31
door klazon
Ik zou zeggen: de ene lijn binnen het kader, en om de blokken heen, of desnoods er tussendoor slingerend.
En de andere lijn buitenom. Dan wordt het letterlijk een voorbeeld van out-of-the-box denken.
Heeft idd weinig met wiskunde te maken.
Re: Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 16:33
door Rogier
Mogen de lijnen oneindig lang zijn?
Bijvoorbeeld zoiets:
<!--graphstart--><script type="text/javascript">graph(-1,1,-2,2,300,300,600,600,'sin(1/x)')</script><!--graphend-->
Re: Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 17:09
door dirkwb
In principe is een lijn oneindig lang, een lijnstuk heeft een eindige lengte, maar wat als dat toegestaan is?
Re: Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 17:51
door hanzwan
Hoe zou oneindige lengte hier helpen? Misschien dat je dan gaat lopen 'rotzooien' met de definitie van lijn. Maar vanuit een topologisch oogpunt zal de ene lijn het vlak in tweeden snijden net als een pizza na het snijden in 2 stukken bestaat. Om dan van stuk A naar B te gaan zonder dit snij stuk te overbruggen is onmogelijk.
Re: Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 18:11
door dirkwb
Ik denk dat ik het heb, een flauwe oplossing:
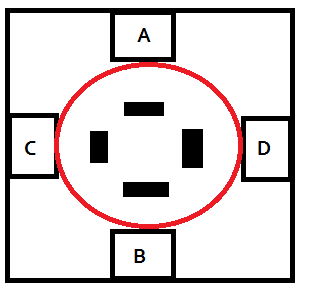
- 1 8570 keer bekeken
Er staat immers niet dat de lijn van A naar B niet door (of beter gezegd langs) D mag gaan. Naar analogie voor de lijn van C naar D. De ljinen snijden mekaar ook niet immers het is één lijn.
Re: Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 18:34
door Rogier
Hoe zou oneindige lengte hier helpen? Misschien dat je dan gaat lopen 'rotzooien' met de definitie van lijn.
Ik dacht aan een of ander limietgeval, bijvoorbeeld een fractal (zoals een
peano kromme) of een dubieuze constructie waarbij het snijpunt onbepaald is o.i.d.
Re: Punten verbinden zonder snijdende lijnen
Geplaatst: vr 27 jan 2012, 18:38
door Drieske
... of een dubieuze constructie waarbij het snijpunt onbepaald is o.i.d.
Ik veronderstel dat je idee hierbij iets à la sin(1/x) is en dan de lijnen door 0 laten gaan (wat losjes geformuleerd, maar je snapt wat ik bedoel?)? Kun je dan nog spreken van een ononderbroken kromme/rechte (wat is de definitie hiervoor?)? Zonee, heb je niet eens nog een rechte die (bijv) A met B verbindt. En ik zou zeggen dat je kromme onderbroken is met sin(1/x).