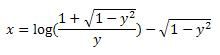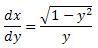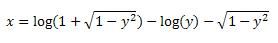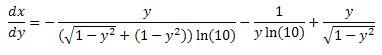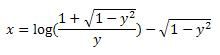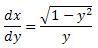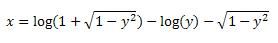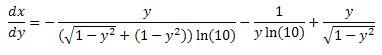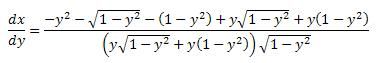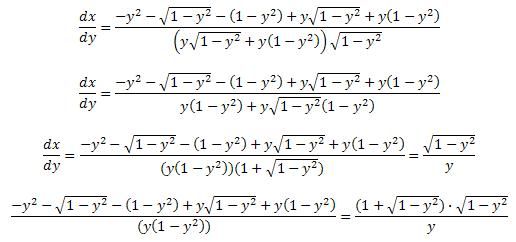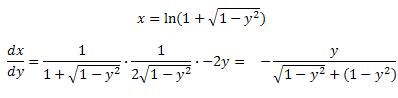1 van 2
Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 19:20
door bramio
Ik heb de volgende formule:
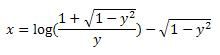
Nu moet ik bewijzen dat de afgeleide van deze formule dit is:
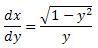
Ik heb eerst de formule omgebouwd:
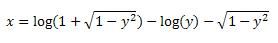
Daarna heb ik het gedifferentieerd (met dubbele kettingregel):
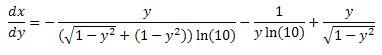
Maar nu heb ik dus moeite met het bewijzen dat de formule in het 4e plaatje gelijk is aan de formule in het 2e plaatje. Zou iemand me hiermee kunnen helpen?
Re: Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 19:40
door tempelier
Ik neem even aan dat alles juist is uitgerekend.
De eerste stap die je dan het beste kan doen is in het laatste antwoord alles onder 1-noemer te brengen.
Want dan kan je de breuken optellen.
PS. De opgave komt toch niet uit een Schaum dictaat want daar bedoelen ze met log gewoon ln?
Re: Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 19:47
door bramio
Ik heb geen idee wat een Schaum dictaat is, dus het zal wel niet het geval zijn.

Klopt, ik zat zelf ook al te denken aan een gelijknamige noemer. Dat is alleen lastig te realiseren, omdat er 2 termen in de eerste breuk staan [(ln(10)*wortel(1-y^2) en ln(10)*(1-y^2)]
Re: Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 19:50
door Safe
Het moet inderdaad ln(...) zijn, maar ga dat na!
Het is trouwens geen dubbele kettingregel, maar kettingregel. Dat je deze herhaald moet toepassen is het gevolg van ´de ketting´. Wat is de ketting hier eigenlijk ...
Re: Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 19:52
door tempelier
bramio schreef: ↑ma 01 okt 2012, 19:47
Ik heb geen idee wat een Schaum dictaat is, dus het zal wel niet het geval zijn.

Klopt, ik zat zelf ook al te denken aan een gelijknamige noemer. Dat is alleen lastig te realiseren, omdat er 2 termen in de eerste breuk staan [(ln(10)*wortel(1-y^2) en ln(10)*(1-y^2)]
Die komen van over Het Grote Water

en daar doen ze dat vaak,
daarom altijd even kijken wat met log bedoeld wordt.
Ja als je vorm correct is krijg je vier factoren in de noemer.
Re: Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 19:58
door bramio
Safe schreef: ↑ma 01 okt 2012, 19:50
Het moet inderdaad ln(...) zijn, maar ga dat na!
Het is trouwens geen dubbele kettingregel, maar kettingregel. Dat je deze herhaald moet toepassen is het gevolg van ´de ketting´. Wat is de ketting hier eigenlijk ...
y = log (u) (of ln (u))
u = 1 + wortel(v)
v = 1-y^2
Re: Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 20:27
door bramio
tempelier schreef: ↑ma 01 okt 2012, 19:52
Die komen van over Het Grote Water

en daar doen ze dat vaak,
daarom altijd even kijken wat met log bedoeld wordt.
Ja als je vorm correct is krijg je vier factoren in de noemer.
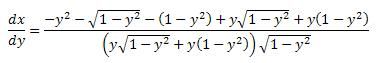
Re: Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 21:04
door dirkwb
Ik sla heel wat stappen over.
Zij:
\( u = \sqrt{1-y^2} \)
dan
\(\frac{dx}{du} = \frac{1}{1-u^2} -1 \)
Tenslotte volgt er:
\( \frac{dx}{du}\frac{du}{dy} = \frac{1-y^2}{y^2}\frac{y}{\sqrt{1-y^2}} \)
Re: Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 21:23
door tempelier
dirkwb schreef: ↑ma 01 okt 2012, 21:04
Ik sla heel wat stappen over.
Zij:
\( u = \sqrt{1-y^2} \)
dan
\(\frac{dx}{du} = \frac{1}{1-u^2} -1 \)
Tenslotte volgt er:
\( \frac{dx}{du}\frac{du}{dy} = \frac{1-y^2}{y^2}\frac{y}{\sqrt{1-y^2}} \)
Dat klopt ja maar het ging er om de twee vormen aan elkaar gelijk te krijgen.
bramio schreef: ↑ma 01 okt 2012, 20:27
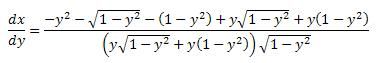
Het is een heidens karwij maar het gaat wel:
Vermenigvuldig de noemer uit en verdrijf er dan de wortel er uit.
Re: Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 22:07
door bramio
Bedoel je zo?
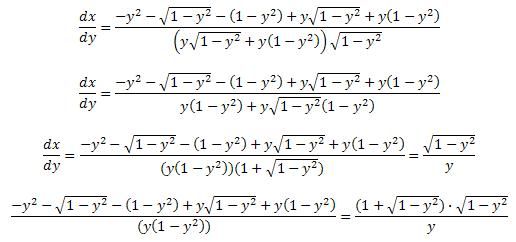
Overigens kan ik nu ook wel beide noemers gelijk maken aan
y, en daarna de ene breuk van de andere breuk halen.
Re: Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 22:08
door tempelier
bramio schreef: ↑ma 01 okt 2012, 22:07
Bedoel je zo?
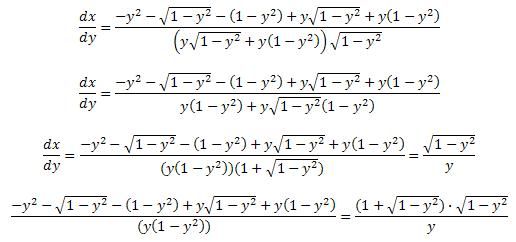
Overigens kan ik nu ook wel beide noemers gelijk maken aan
y, en daarna de ene breuk van de andere breuk halen.
Ja.
De antwoorden kloppen niet met elkaar,
de manier is echter wel goed dus moet er ergens een reken fout zijn
Re: Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 22:25
door bramio
Heb ik deze misschien incorrect gedifferentieerd? Dit is die kettingregel waar ik het eerder over had.
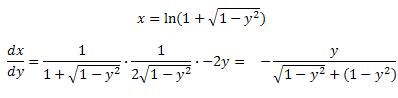
Re: Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 22:36
door tempelier
bramio schreef: ↑ma 01 okt 2012, 22:25
Heb ik deze misschien incorrect gedifferentieerd? Dit is die kettingregel waar ik het eerder over had.
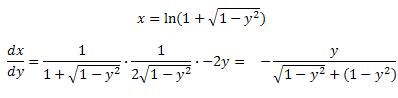
Dit is goed ik heb het op de hand bekeken en voor de zekerheid met Maple gecontroleerd.
Re: Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 22:40
door bramio
Hmm, dan zal ik het foutje elders hebben gemaakt. Maar de methode is verder goed? Dan zal ik morgen nog even grondig mijn berekeningen nalopen, het begint namelijk al laat te worden.

Zeer dank voor de hulp!

Re: Bewijzen dat twee formules gelijk zijn
Geplaatst: ma 01 okt 2012, 22:53
door tempelier
Ja de methode is goed (wel omslachtig) maar ik zie de fout ook niet zo snel.
Slaap wel.