1 van 1
Hoeksnelheid berekenen
Geplaatst: wo 28 nov 2012, 14:09
door brue
Hallo allemaal,
Ik wil graag een bepaalde hoeksnelheid berekenen. Ik heb in mn hoofd een idee dat het iets moet zijn dat lijkt op wat je hebt als je iets recht omhoog gooit.
Als je iets recht omhoog gooit heb je namelijk een beginpunt, een beginsnelheid en een versnelling naar beneden. Dit komt dan neer op y(t)=y0+v0t+1/2gt2 met als snelheid v(t)=v0+gt. Hierbij is y0 gegeven, g is gegeven, v0is gegeven.
Nu over de hoeksnelheid.
Ik heb een hoek theta0=0, een hoeksnelheid theta[punt]0=0 en een gegeven hoekversnelling van theta[dubbelpunt](theta)=c*cos(theta). (even toelichting over de hoekversnelling, deze is afhankelijk van de hoek, op het begin is de hoekversnelling dus gelijk aan c).
Nu dacht ik aan integreren en differentieren dat de hoek dan gegeven zou worden door
theta(t)=theta0+theta[punt]0*t+1/2*(c*cos(theta))*t2
=1/2*(c*cos(theta))*t2
En dan loop ik dus vast, want dan weet ik nog niet wat de snelheid is bij een gevraagde t, of een gevraagde hoek.
Alvast bedankt, Ray
Re: Hoeksnelheid berekenen
Geplaatst: wo 28 nov 2012, 16:37
door physicalattraction
Het grote verschil tussen beide gevallen is dat in het eerste geval je de versnelling als constant beschouwt, en in het tweede geval laat variëren met de huidige hoek. De eerste kun je daardoor simpelweg integreren (
\(\int \int a \ \mbox{d}t \ \mbox{d}t = a t^2\)
), maar bij de tweede ga je de mist in. De integraal
\(\int \int c \cdot \cos(\theta) \ \mbox{d}t \ \mbox{d}t\)
is namelijk niet
\(c \cdot \cos(\theta) t^2\)
, daar de variabele
\(\theta\)
zelf ook van
\(t\)
afhangt. Deze moet je dan ook oplossen met een
differentiaalvergelijking. Ben je hier bekend mee?
PS: Het is duidelijker als je je formules in LaTeX typt. Zie
hier voor een handleiding, of klik op mijn formules voor voorbeelden.
Re: Hoeksnelheid berekenen
Geplaatst: wo 28 nov 2012, 17:34
door brue
Ik heb differentiaalvergelijkingen een beetje gehad op de studie, was het meer los
dit op, in plaats dat we ze zelf op moesten stellen.
Als ik mijn hersens pijnig kom ik dan op iets voor de hoek:
\(\theta=\theta_0+\int\dot{\theta}+\int\int\ddot{\theta}\)
En voor de hoeksnelheid van
\(\dot{\theta}=\dot{\theta}_0+\int\ddot{\theta}\)
Maar als ik dan voor mijn hoekversnelling een formule van
\(\ddot{\theta}=cos(\theta)*g*\frac{L_1*m_1-L_2*m_2}{L_1^2*m_1+L_2^2*m_2}
\)
bekijk waarbij
\(m_1, m_2\)
vaste waarden zijn en
\(L_2\)
op zijn tijd weer 2.5x
\(L_1\)
is, zie ik eigenlijk door de bomen het bos niet meer

Zou je me op weg kunnen helpen

?
Re: Hoeksnelheid berekenen
Geplaatst: wo 28 nov 2012, 17:54
door physicalattraction
Zo te zien is in de uitdrukking voor
\(\ddot{\theta}\)
alleen
\(\theta\)
zelf afhankelijk van de tijd. De overige waarden kun je in een grote variabele stoppen, zodat je hier geen last meer van hebt. Vervolgens gebruik je dan jouw eerste formule.
Let wel op: deze is een beetje slordig. Die
\(\dot{\theta}\)
moet de beginsnelheid representeren, dus beter kun je noteren:
\(\theta=\theta_0+\int\dot{\theta_0} \ \mbox{d}t+\int\int\ddot{\theta} \ \mbox{d}t \ \mbox{d}t\)
Re: Hoeksnelheid berekenen
Geplaatst: wo 28 nov 2012, 20:36
door brue
physicalattraction schreef: ↑wo 28 nov 2012, 17:54
Zo te zien is in de uitdrukking voor
\(\ddot{\theta}\)
alleen
\(\theta\)
zelf afhankelijk van de tijd
Dit stukje begrijp ik even niet. Bedoel je dat alleen
\(\theta\)
afhankelijk is van de tijd, omdat
\(\ddot{\theta}\)
afhankelijk is van de hoek.
Als dit zo is, dan is
\(\int\ddot{\theta}dt\)
toch gelijk aan
\(cos(\theta)*g*\frac{L_1*m_1-L_2*m_2}{L_1^2*m_1+L_2^2*m_2}*t\)
omdat
\(g*\frac{L_1*m_1-L_2*m_2}{L_1^2*m_1+L_2^2*m_2}\)
in principe gewoon een constance 'c' is(deze waarden wijzigen niet tijdens de draaiing)?
Edit: Ik zie al wat je bedoelt, maar hoe moet ik dan verder. Ik kan niet die
\(\theta\)
invullen in die uitdrukking voor
\(\ddot{\theta}\)
want dan blijf je eeuwig doorgaan.
Re: Hoeksnelheid berekenen
Geplaatst: do 29 nov 2012, 00:00
door brue
Sorry voor de dubbele post.
Wat ik nu denk is het volgende:
De hoek
\(\theta\)
wordt als volgt weergeven:
\( \theta(t)=\theta_0+\int\dot{\theta_0} \ \mbox{d}t+\int\int\ddot{\theta} \ \mbox{d}t \ \mbox{d}t \)
De hoeksnelheid
\(\ddot{\theta}\)
wordt weergeven door:
\( \dot{\theta}(t)=\dot{\theta_0}+\int\ddot{\theta} \ \mbox{d}t \)
De hoekversnelling door:
\( \ddot{\theta}(t)=\ddot{\theta}=cos(\theta)*g*\frac{L_1*m_1-L_2*m_2}{L_1^2*m_1+L_2^2*m_2} \)
Dan is
\(\int\ddot{\theta} \ \mbox{d}t =cos(\theta)*g*\frac{L_1*m_1-L_2*m_2}{L_1^2*m_1+L_2^2*m_2}*t\)
en
\(\int\int\ddot{\theta} \ \mbox{d}t \ \mbox{d}t =cos(\theta)*g*\frac{L_1*m_1-L_2*m_2}{L_1^2*m_1+L_2^2*m_2}*t^2\)
Je weet dat
\(\dot{\theta_0}=0\)
dus de integraal hiervan is 0
Dan is de uiteindelijke formule voor hoek
\(\theta\)
:
\( \theta(t)=\theta_0+cos(\theta)*g*\frac{L_1*m_1-L_2*m_2}{L_1^2*m_1+L_2^2*m_2}*t^2\)
en de formule voor
\(\dot{\theta}\)
:
\( \dot{\theta}(t)=cos(\theta)*g*\frac{L_1*m_1-L_2*m_2}{L_1^2*m_1+L_2^2*m_2}*t\)
Als we nu zeggen dat
\(\theta_0=30^\circ\)
en
\(c=g*\frac{L_1*m_1-L_2*m_2}{L_1^2*m_1+L_2^2*m_2}=1\)
wat moet ik dan nog doen om de hoek en hoeksnelheid voor tijd t te weten?
Re: Hoeksnelheid berekenen
Geplaatst: do 29 nov 2012, 09:26
door physicalattraction
De hoeksnelheid
\(\ddot{\theta}\)
wordt weergeven door:
\( \theta(t)=\theta_0+cos(\theta)*g*\frac{L_1*m_1-L_2*m_2}{L_1^2*m_1+L_2^2*m_2}*t^2\)
Nu maak je helaas toch weer de fout door te integreren naar
\(t\)
zonder er rekening mee te houden dat
\(\theta\)
van de tijd afhangt.
Laten we beginnen vanuit de eerste vergelijking:
\(\theta(t)=\theta_0+\int\dot{\theta_0} \ \mbox{d}t+\int\int\ddot{\theta} \ \mbox{d}t \ \mbox{d}t\)
Nu differentiëren we twee keer naar de tijd. De beginvoorwaarden
\(/theta_0\)
en
\(\cdot{theta}\)
worden hiermee irrelevant, maar die hebben we later nodig om de juiste integratieconstanten te bepalen.
\(\frac{\partial^2 \theta}{\partial t}(t) = \ddot{\theta}(t) \rightarrow \frac{\partial^2 \theta}{\partial t}(t) = c \cdot \cos(\theta(t))\)
Je hebt nu de algemene vorm van de differentiaalvergelijking te pakken. Deze is echter verre van triviaal om op te lossen, daar deze niet lineair is. Een soortgelijke vergelijking kun je
hier vinden voor een slinger, maar dan met een sinus i.p.v. een cosinus. Ben je ook met een slinger bezig en heb je misschien je hoek anders gedefinieerd dan in het voorbeeld aldaar?
Re: Hoeksnelheid berekenen
Geplaatst: do 29 nov 2012, 11:33
door brue
Het gaat eigenlijk om een arm, waar 2 verschillende gewichten op staan en een resultant moment is, begint bij 70-60 graden en eindigd bij -70-80 graden, afhankelijk van wat de snelheid daar is.
De formule die je nu dus hebt opgeschreven
\( \frac{\partial^2 \theta}{\partial t}(t) = \ddot{\theta}(t) \rightarrow \frac{\partial^2 \theta}{\partial t}(t) = c \cdot \cos(\theta(t)) \)
is dan vergelijkbaar met

die in die wikipagina staat. Maar dan nemen ze daar aan dat

omdat

maar
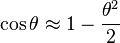
geldt niet voor deze functie omdat

niet geld.
Dus dan is die wikipagina ook niet te gebruiken toch

?
PS. is het niet
\( \frac{\partial^2 \theta}{\partial t^2}(t) =\)
PPS. Is er geen manier dat ik dit in wolfram of matlab kan gooien? Ik heb wel differentiaalvergeleikingen (heel even) gehad, maar ik heb het idee dat ik hier weer net te weinig kennis voor heb.
Re: Hoeksnelheid berekenen
Geplaatst: do 29 nov 2012, 12:03
door physicalattraction
Ik vraag me in dat geval af of er überhaupt wel een analytische oplossing mogelijk is voor willekeurige hoek
\(\theta\)
. Je kunt hem natuurlijk wel in Matlab gooien, dan kun je hem numeriek oplossen. Ik weet niet meer precies hoe dat ging, maar je moet eens in de help functie zoeken naar 'ode45'.
Het is trouwens inderdaad
\(\frac{\partial^2 \theta}{\partial t^2}(t)\)
, dat kwadraatje was ik vergeten erbij te zetten.
Re: Hoeksnelheid berekenen
Geplaatst: vr 30 nov 2012, 17:16
door pgbakker
Omdat t niet expliciet in de DV voorkomt kun je wel een eerste integraal vinden van deze DV.
Dit gaat als volgt:
De DV luidt d2(theta) dt2 = c*cos(theta)
Noem p=d(theta)/dt, dan geldt d2(theta)/dt2 = dp/dt
De DV wordt dan dp/dt = c*cos(theta).
Nu t elimineren , dan volgt de eerste orde DV:
dp/d(theta)= c*cos(theta)/p
Deze DV kun je integreren.
Succes.
pgb
Re: Hoeksnelheid berekenen
Geplaatst: za 01 dec 2012, 20:26
door physicalattraction
\(\frac{\partial p}{\partial \theta} = c \cdot \frac{\cos(\theta)}{p}\)
Deze DV kun je integreren.
Interessant oplossingsmethodiek, maar ik zie hem nog niet helemaal. Hoe kun je deze uitdrukking integreren? Want
\(p\)
hangt hier van
\(\theta\)
af op een manier die je niet weet (deze probeer je namelijk te bepalen). Dat was (in een ander jasje) eigenlijk ook waar de TS oorspronkelijk tegenaan liep: de afgeleiden zelf hangen op een niet-triviale manier van de tijd af.
Re: Hoeksnelheid berekenen
Geplaatst: za 01 dec 2012, 22:10
door pgbakker
Hallo,
Eerst een opmerking vooraf.
Onze DV bevat t niet expliciet, p hangt dus niet expliciet van t af maar wel expliciet van theta.
Je kunt de partiële d's vervangen door rechte d's.
We krijgen dan: dp/d(theta) = c*cos(theta)/p
Nu variabelen scheiden, dwz alles met p naar links en alles met theta naar rechts van het = teken.
We krijgen dan: pdp = c*cos(theta)d(theta)
Je kunt nu links en rechts van het = teken integreren.
Dit geeft je p expliciet als functie van theta.
Succes.
Laat even weten of het gelukt is.
Gr. pgb
Re: Hoeksnelheid berekenen
Geplaatst: di 04 dec 2012, 16:06
door physicalattraction
Hoewel je laatste opmerking wellicht aan de TS gericht is, kom ik er zelf ook nog niet uit. Ik heb nu:
\( p dp = c \cdot \cos(\theta) d\theta\)
\( \frac{1}{2} p^2 = -c \cdot \sin(\theta) + C\)
\( \Bigl(\frac{d \theta}{d t}\Bigr)^2 = -2c \cdot \sin(\theta) + C\)
Maar hoe ga je nu verder om een functievoorschrift
\(\theta(t)\)
te verkrijgen?
Re: Hoeksnelheid berekenen
Geplaatst: di 04 dec 2012, 18:01
door pgbakker
Er is bij het integreren een tekenfout opgetreden. Wanneer je cos() integreert levert dat +sin() op.
We hebben dus:
\(
\Bigl(\frac{d \theta}{d t}\Bigr)^2 = 2c \cdot \sin(\theta) + C
\)
Dit noemen we de eerste integraal, het beschrijft het functionele verband tussen hoeksnelheid d(theta)d(t) en theta.
Nu beginvoorwaarden invullen: t=0, theta = 0, d(theta)/dt = 0. Dit geeft C=0.
Het expliciete verband theta(t) volgt door nog een keer te integreren. De tweede integraal zeg maar.
Dit gaat door opnieuw variabelen scheiden: alles met t naar links en alles met theta naar rechts.
Dit geeft inprincipe:
t = int(d(theta)/sqr(2c.sin(theta)) + const.
Dit is een elliptische integraal waar we geen analytische uitdrukking voor hebben.
Wil je verder dan is numerieke integratie een aanpak.
pgb
Re: Hoeksnelheid berekenen
Geplaatst: wo 05 dec 2012, 10:13
door physicalattraction
Het lijkt allemaal zo simpel als je het uitlegt. Bedankt!
 die in die wikipagina staat. Maar dan nemen ze daar aan dat
die in die wikipagina staat. Maar dan nemen ze daar aan dat  omdat
omdat  maar
maar 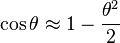 geldt niet voor deze functie omdat
geldt niet voor deze functie omdat