1 van 2
Hoogtelijn in een driehoek berekenen.
Geplaatst: di 01 jul 2014, 19:58
door jor177
Hallo allemaal.
Een tijdje terug zat ik met mijn vader te praten over een aantal wiskundige onderwerpen.
Uiteindelijk kwam er papier en pen bij het gesprek en legde hij mij een opgave voor om te maken.
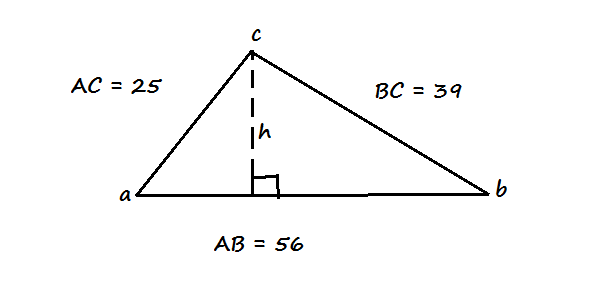
Alle zijdes zijn gegeven, en je moet h zien te berekenen.
Mijn vader kwam uit op h = 15
En dat klopt.
Hij zegt dat hij het zichzelf heeft aangeleerd.
Eventueel kan ik ook nog zijn uitwerkingen posten.
Maar mijn vraag is nu: hoe heet de stelling? of waarmee dit kan worden bewezen?
Ik heb zelf al iets van: projectie stelling of de stelling van thales gevonden.
Ik zou graag van jullie willen weten wat het juiste is..
Re: Hoogtelijn in een driehoek berekenen.
Geplaatst: di 01 jul 2014, 20:45
door kwasie
Met de cosinusregel kun je een hoek berekenen, en vervolgens met is h te berekenen sin(alfa) = h / AC
Re: Hoogtelijn in een driehoek berekenen.
Geplaatst: di 01 jul 2014, 21:56
door Safe
De hint van kwasie heeft zin als je iets van goniometrie weet.
Je kan het voetpunt van de hoogtelijn d noemen en dan stellen we (bv) ad=p en bd=q ...
Wat kan je nu opschrijven van p+q=...
Verder heb je twee rechthoekige driehoeken, welke stelling geldt dan in beide driehoeken, schrijf dat op ...
Re: Hoogtelijn in een driehoek berekenen.
Geplaatst: di 01 jul 2014, 22:10
door aadkr
nu ben ik geen echte wiskundige, maar je kunt ook het oppervlak van deze driehoek berekenen met een zekere formule.
begrijp je welke formule ik bedoel?
als je de lengte van de 3 zijden bij elkaar optelt en het resultaat door 2 deelt krijg je 60 , en dat is geen toeval
nu ik Safe zijn bericht zie, moet je mijn bericht maar even als niet geschreven beschouwen.
niet dat de oplossingsmethode die mij voor ogen staat fout is , maar de oplossingsmethode van Safe is veel mooier .
Re: Hoogtelijn in een driehoek berekenen.
Geplaatst: wo 02 jul 2014, 01:58
door Th.B
Heron behoort wel tot de mogelijkheden, maar het is een erg onbekende stelling.
Re: Hoogtelijn in een driehoek berekenen.
Geplaatst: wo 02 jul 2014, 18:16
door tempelier
jor177 schreef:
Hallo allemaal.
Een tijdje terug zat ik met mijn vader te praten over een aantal wiskundige onderwerpen.
Uiteindelijk kwam er papier en pen bij het gesprek en legde hij mij een opgave voor om te maken.

Alle zijdes zijn gegeven, en je moet h zien te berekenen.
Mijn vader kwam uit op h = 15
En dat klopt.
Hij zegt dat hij het zichzelf heeft aangeleerd.
Eventueel kan ik ook nog zijn uitwerkingen posten.
Maar mijn vraag is nu: hoe heet de stelling? of waarmee dit kan worden bewezen?
Ik heb zelf al iets van: projectie stelling of de stelling van thales gevonden.
Ik zou graag van jullie willen weten wat het juiste is..
Je vader heeft hem vermoedelijk uitgerekend met een variant van de s-formule.
Zo zou ik het ook gedaan hebben.
Daar komt geen goniometrie aan te pas.
Wel is de formule wat in de vergetelheid geraakt.
Hij is snel gevonden als je er naar zoekt, lukt het niet dan wil ik je hem wel geven.
Re: Hoogtelijn in een driehoek berekenen.
Geplaatst: wo 02 jul 2014, 18:37
door Safe
tempelier schreef:
Je vader heeft hem vermoedelijk uitgerekend met een variant van de s-formule.
Vermoedelijk niet ... , didactisch is dat niet verantwoord!
Re: Hoogtelijn in een driehoek berekenen.
Geplaatst: wo 02 jul 2014, 18:40
door tempelier
Safe schreef:
Vermoedelijk niet ...
Voor de Mammoet wet was die methode standaard.
Re: Hoogtelijn in een driehoek berekenen.
Geplaatst: wo 02 jul 2014, 19:02
door jor177
Ik zal wel even kijken of ik het papiertje waar hij dit op uit heeft geschreven kan vinden.
Re: Hoogtelijn in een driehoek berekenen.
Geplaatst: wo 02 jul 2014, 19:34
door jor177
Hier heb ik de uitwerkingen gevonden. Volgens mij doet hij eerst de stelling van Pythagoras

Re: Hoogtelijn in een driehoek berekenen.
Geplaatst: wo 02 jul 2014, 19:36
door Safe
Dat kan wel iets eenvoudiger ... , heb je m'n aanwijzing al gevolgd?
Heb je misschien vragen over bovenstaande uitwerking, want die is uitstekend!
Re: Hoogtelijn in een driehoek berekenen.
Geplaatst: wo 02 jul 2014, 20:22
door aadkr
uiteraard gebruikt je vader de stelling van pythagoras.
dat is ook de bedoeling van Safe dat je die gebruikt.
de oplossing die Safe voor ogen staat is geniaal in zijn eenvoud.
volg dus a.u.b. de raad van Safe op .
om een begin te maken geldt natuurlijk dat p+q=56
Re: Hoogtelijn in een driehoek berekenen.
Geplaatst: wo 02 jul 2014, 20:31
door tempelier
Safe schreef:
Vermoedelijk niet ... , didactisch is dat niet verantwoord!
Waarom is die formule didactisch niet verantwoord?
Re: Hoogtelijn in een driehoek berekenen.
Geplaatst: wo 02 jul 2014, 21:52
door Safe
tempelier schreef:
Waarom is die formule didactisch niet verantwoord?
Wiskunde is niet het 'blind' invullen van formules. Deze formule zou dus netjes afgeleid moeten worden. Dat past tegenwoordig niet meer in het (meetkunde)programma. Ziedaar ...
Re: Hoogtelijn in een driehoek berekenen.
Geplaatst: do 03 jul 2014, 19:17
door tempelier
Safe schreef:
Wiskunde is niet het 'blind' invullen van formules. Deze formule zou dus netjes afgeleid moeten worden. Dat past tegenwoordig niet meer in het (meetkunde)programma. Ziedaar ...
Dat is onzin.
De formule werd indertijd wel degelijk afgeleid.
Ook is het meten met twee maten, wil je dan pas goniomtrie invoeren als je de waarden met de een of andere reeks kunt afleiden?
Wie kan er op de middelbare school nog handmatig een tweedegraads wortel trekken om van de derdemachts wortel maar te zwijgen.


