1 van 2
uitrekking van een veer
Geplaatst: za 30 aug 2014, 11:42
door egos
Wanneer een bepaalde massa aan een verticale veer wordt opgehangen, wordt de veer dan bovenaan meer uitgerekt dan onderaan?
Met andere woorden heeft de veer bovenaan de grootste elasticiteit en onderaan de minste elasticiteit en bovenaan de minste compliantie en onderaan de meeste, zoals in de afbeelding is aangegeven?
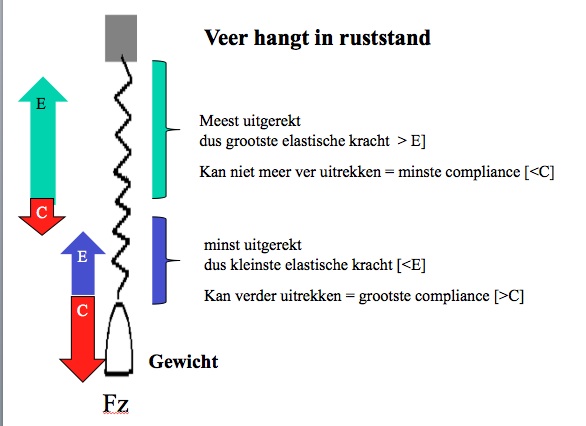
- veer 2108 keer bekeken
Re: uitrekking van een veer
Geplaatst: za 30 aug 2014, 12:07
door Anton_v_U
Wat een leuke vraag.
Een veer rekt net zo uit als een elastiek. Pak een elastiek, knip het open en leg het neer in een rechte lijn zonder dat je het uitrekt. Zet dan twee blauwe strepen op de onderste helft, 2 cm uit elkaar en twee rode strepen op de bovenste helft, ook 2 cm uit elkaar.
Zet ergens in het midden 2 groene strepen, bijv. 3 cm uit elkaar.
Maak één kant van het elastiek vast en rek het uit tot de dubbele lengte. Hoever zitten de blauwe strepen nu uit elkaar? En de rode? En de groene?
Maakt het uit of je het elastiek verticaal houdt?
Wat is je conclusie? Waar rekt het elastiek het meeste uit?
[edit] Als je nog twijfelt welke kant het meeste uitrekt:
Maak de andere kant van het elastiek vast en beantwoord dezelfde vragen.
Re: uitrekking van een veer
Geplaatst: za 30 aug 2014, 14:40
door egos
Als ik een veer of een elastiek bij de hand had, zou ik idd proefondervindelijk zelf het antwoord hebben gevonden.
Omdat ik beide niet voorhanden heb, heb ik de vraag op dit forum gesteld.
Zoals je de proef voorstelt zou ik, zonder dat ik hem uitvoer, bijna concluderen dat de elastiek overal even ver uitrekt.
Verticaal of horizontaal maakt niet uit.
Hetzelfde zou voor de veer gelden ook al hangt er een gewicht aan.
Juiste conclusie?
Re: uitrekking van een veer
Geplaatst: za 30 aug 2014, 17:24
door Flisk
Bij een elastiek zou het niet veel uitmaken. Een veer heeft natuurlijk ook zijn eigen gewicht. Dus het bovenste gedeelte van de veer draagt meer gewicht dan het onderste. Zou het hiermee te maken hebben?
Re: uitrekking van een veer
Geplaatst: za 30 aug 2014, 17:41
door Michel Uphoff
Zou het hiermee te maken hebben?
Dat moet wel. Een massaloze veer bestaat niet, hoewel we de eigen massa in een aantal situaties kunnen verwaarlozen.
Daar waar de massa van het gewicht niet veel groter, of zelfs kleiner is tov van die van de veer, mag je niet verwaarlozen.
Het is dus
of een slim gestelde vraag, want men houdt rekening met de eigen massa van de veer,
of als die massa niet mee mag tellen een apert foutieve voorstelling van zaken.
Re: uitrekking van een veer
Geplaatst: za 30 aug 2014, 18:29
door aadkr
mag ik een domme vraag stellen?
wat wordt hier bedoeld met het woord compliantie?
Re: uitrekking van een veer
Geplaatst: za 30 aug 2014, 18:44
door Michel Uphoff
Compliance betekent ook iets als toegeeflijkheid. Staat voor rek in meters per Newton.
Re: uitrekking van een veer
Geplaatst: za 30 aug 2014, 19:06
door Anton_v_U
egos schreef:
Juiste conclusie?
Helemaal goed, dat is de basissituatie.
Inderdaad, als de massa van de veer niet verwaarloosbaar is, moet je er rekening mee houden (als je de veer verticaal houdt). Maar dan nog: als je de lengte in onbelaste vorm als nul-lengte neemt (dus het uitrekken door het eigen gewicht is al verdisconteerd) dan mag je bij redelijke benadering rekenen met een ideale veer waarin de relatieve lengteverandering over elk stukje veer hetzelfde is.
Bij het dynamische gedrag (bijv. trillingstijd) moet je wel altijd de massa van de veer meenemen tenzij die verwaarloosbaar is t.o.v. de massa die er aan hangt.
Re: uitrekking van een veer
Geplaatst: za 30 aug 2014, 19:09
door Jan van de Velde
aadkr schreef:
wat wordt hier bedoeld met het woord compliantie?
Kende het ook niet, dus ik vertaalde het letterlijk naar engels en gooide het in google:
wikipedia
The inverse of spring rate is compliance, that is: if a spring has a rate of 10 N/mm, it has a compliance of 0.1 mm/N.
Re: uitrekking van een veer
Geplaatst: za 30 aug 2014, 19:15
door egos
Elasticiteit is de weerstand tegen uitrekking
Compliantie is het vermogen, waarin toegegeven wordt aan vormverandering, maw de uitrekbaarheid
Re: uitrekking van een veer
Geplaatst: za 30 aug 2014, 19:24
door Anton_v_U
Ik kende het begrip ook niet. Is dus analoog aan het verband tussen elektrische weerstand en geleidbaarheid: als je stukjes veer in serie zet (achter elkaar schakelt) moet je de compliantie optellen en als je ze parallel zet moet je de veerconstante optellen.
Re: uitrekking van een veer
Geplaatst: za 30 aug 2014, 19:36
door egos
Anton_v_U schreef:
Helemaal goed, dat is de basissituatie.
Maar dan nog: als je de lengte in onbelaste vorm als nul-lengte neemt (dus het uitrekken door het eigen gewicht is al verdisconteerd) dan mag je bij redelijke benadering rekenen met een ideale veer waarin de relatieve lengteverandering over elk stukje veer hetzelfde is.
Oké! Wanneer ik deze theorie gebruik voor het volume van de longblaasjes, dan zouden de alveolen in de longtoppen net zo ver uitgetrokken worden als de alveolen in de longbasis.
</blockquote>
Toch blijkt in de praktijk, dat de longblaasjes in de longtoppen een groter volume hebben dan in de longbasis.
De longblaasjes in de longtop hebben dus de grootste elasticiteit (meeste weerstand tegen de uitrekking) en de minste compliantie (kunnen dus niet meer verder uitrekken).
Ik heb van jou begrepen, dat ik in deze niet de vergelijking met de veer mag maken en moet de verklaring voor het grotere volume van de longblaasjes in de longtoppen ergens anders zoeken.
Re: uitrekking van een veer
Geplaatst: za 30 aug 2014, 19:37
door Jan van de Velde
Michel Uphoff schreef:
Het is dus
of een slim gestelde vraag, want men houdt rekening met de eigen massa van de veer,
of als die massa niet mee mag tellen een apert foutieve voorstelling van zaken.
ik denk dat dit een feitelijk antwoord op de vragen in de startpost is
Re: uitrekking van een veer
Geplaatst: za 30 aug 2014, 19:49
door Jan van de Velde
egos schreef:
De longblaasjes in de longtop hebben dus de grootste elasticiteit (meeste weerstand tegen de uitrekking) en de minste compliantie (kunnen dus niet meer verder uitrekken).
Ik denk dat hier misverstanden gaan ontstaan, nog niet per se over die longblaasjes, maar wel over de terminologie.
Elasticiteit is NIET weerstand tegen uitrekking. Ervan uitgaande dat de uitrekking nergens in de veer tegen praktisch/materiaaltechnische grenzen aanloopt kost het net zoveel EXTRA kracht om een bijna ontspannen veer een centimetertje VERDER uit te rekken als dat het kost om een half uitgerekte veer een centimetertje verder uit te rekken.
Verder heb ik de indruk dat hier met elasticiteit eigenlijk veerconstante wordt bedoeld, en dat is gewoon een veereigenschap, en zoals hierboven uitgelegd binnen praktische grenzen onafhankelijk van uitrekking.
Omdat
compliantie de inverse is geldt mutatis mutandis voor deze eigenschap hetzelfde. Bovenin zal eenzelfde extra extra uitrekking ook duiden op een gelijke extra uitgeoefende kracht als onderin de situatie zoals in de startpost getekend.
En vervolgens wordt de vraag volgens mij een biologische: zijn longblaasjes bij benadering te vergelijken met (ideale) veren?
Re: uitrekking van een veer
Geplaatst: za 30 aug 2014, 19:55
door Anton_v_U
egos schreef:
Toch blijkt in de praktijk, dat de longblaasjes in de longtoppen een groter volume hebben dan in de longbasis.
Lijkt me een veel te ingewikkeld systeem om met een min of meer homogene veer te benaderen. In de eerste plaats zijn de longen niet overal even breed. Als aan elastiekje plaatselijk dunner is, dan zal dat stuk verder oprekken als het elastiekje onder spanning staat. Ten tweede vraag ik me af of de longblaasjes overal exact dezelfde eigenschappen hebben. Misschien heeft de natuur het om één of andere reden zo geregeld dat die dingen niet overal dezelfde eigenschappen hebben. Tot slot gaat het niet om uitrekken in de lengterichting maar in alle richtingen tegelijk net als een ballon. Het doel is immers om het volume te vergroten zodat die dingen zich volzuigen.