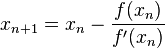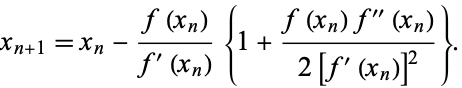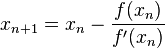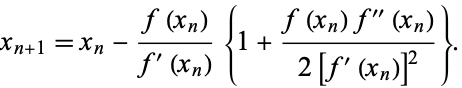sciencetalk

De Newton-Raphson methode leidt tot de volgende formule:
 

 
Nu moeten we op ongeveer eenzelfde wijze tot de volgende formule komen:
 

 
We komen hier echt niet uit, wie kan ons helpen??
.
 

Je zou Newton-Raphson kunnen zien als een lineaire, eerste orde benadering, i.e. f(x+h) ≈ f(x) + h f'(x). Daar je de nulpunten zoekt van je functie f, heb je dus eigenlijk: 0 = f(x + h) ≈ f(x) + h f'(x) of nog h = -f(x)/f'(x). Daar x+h het nulpunt is, weten we dat x+h ≈ x - f(x)/f'(x). Hier maken we nu een iteratieve formule van en we bekomen Newton-Raphson:  
De volgende stap zou zijn om geen lineaire, maar tweede orde benadering te beschouwen, i.e. f(x+h) ≈ f(x) + h f'(x) + h² f''(x)/2. Opnieuw oplossen naar h geeft Nu nog een truukje toepassen: de reeksontwikkeling: en dit gebruiken en jouw formule geeft (let op de veranderingen! zeker in de accentjes ) en dus zoals eerder bekom je als (iteratieve) benadering voor je nulpunt dat  
Er zijn uiteraard veel manieren om dit af te leiden. Een hint voor een andere manier:

• Pas Newton-Raphson toe op de functie
  \(g(x) = \frac{f(x)}{\sqrt{|f'(x)|}}\)
  (merk op dat als f(x) = 0 én f'(x) ≠ 0 dan is g(x) = 0 en omgekeerd, als g(x) = 0 dan is f(x) = 0).

Hopelijk heb je hier iets aan. 
 
Maar uit je titel maak ik op dat je ook de convergentie moet bespreken?

Hoi Drieske, 
superbedankt voor je uitleg, ik heb er veel aan!
Ik snap alleen nog niet hoe je bepaalt of je de + of - versie van de abc-formule moet gebruiken.
Jij hebt de +-versie gebruikt, maar waarom?
Ik hoef verder de convergentie niet te bespreken (denk ik), de vraag is hoe deze kubische convergentiemethode tot stand is gekomen.
 

Je wilt dat h zo klein mogelijk is. Dat is bij de +-versie het geval.
 
Misschien even wat meer details: je hebt dus  en je wilt dat deze h zo klein mogelijk is. Maar wat "zo klein mogelijk is", hangt momenteel af van het teken van f'(x). Dat los je op door te delen door f'(x) en je krijgt dan

Waarom hangt het teken van f'(x) af? Het lijkt me dat het ook van f''(x) af kan hangen?
En bij wegdelen blijft alsnog een f'(x) term (en een f''(x) term) staan?

Okee, beter uitgedrukt: je wilt de teller zo klein mogelijk. Omdat je niet weet of f'(x) positief of negatief is, weet je dus ook niet of je nu de + of de - wilt. Maar als er nu -1 staat, dan is het wél duidelijk welke oplossing je teller klein maakt (veronderstellende dat f'(x) niet 0 is!)...

 

Mocht je je niet comfortabel voelen met deze aanpak, is er een work-around (die geen reeksen e.d. gebruikt). Je vertrekt dan weer van f(x+h) = f(x) + f'(x) h + f''(x) h²/2, maar je schrijft nu:
Gebruiken dat (zie Newton-Raphson) h = -f(x)/f'(x), geeft je dat 
[/size]
of dus
[/size]
Nu is het gewoon wat spelen met dit en je bent er.