1 van 1
vertraging bij impact
Geplaatst: za 07 mar 2015, 16:31
door Willemhoeylaerts
Voor mijn GIP heb ik een aantal vragen opgesteld en ben deze nu aan het oplossen maar zit ergens mee in.
Het komt er op neer: een snowboarder neemt een wip met een bepaalde snelheid en zal dan landen op een ijzeren rail met die snelheid! daarna zal hij dan ook gaan vertragen door de wrijvingskracht tussen het snowboard en de rail maar dat is niet het probleem.
Mijn vraag is: als de snowboarder landt op de rail, zorgt die impact dat hij heeft ook voor een vertraging? of moet je die verwaarlozen en alleen rekening houden met de vertraging die ''achteraf'' wordt veroorzaakt door de wrijvingskracht?
de snelheid waarmee hij op de rail belandt is 5,6 m/s
de massa is 80 kg
de invalshoek is 35 graden
+ zie foto bijlage
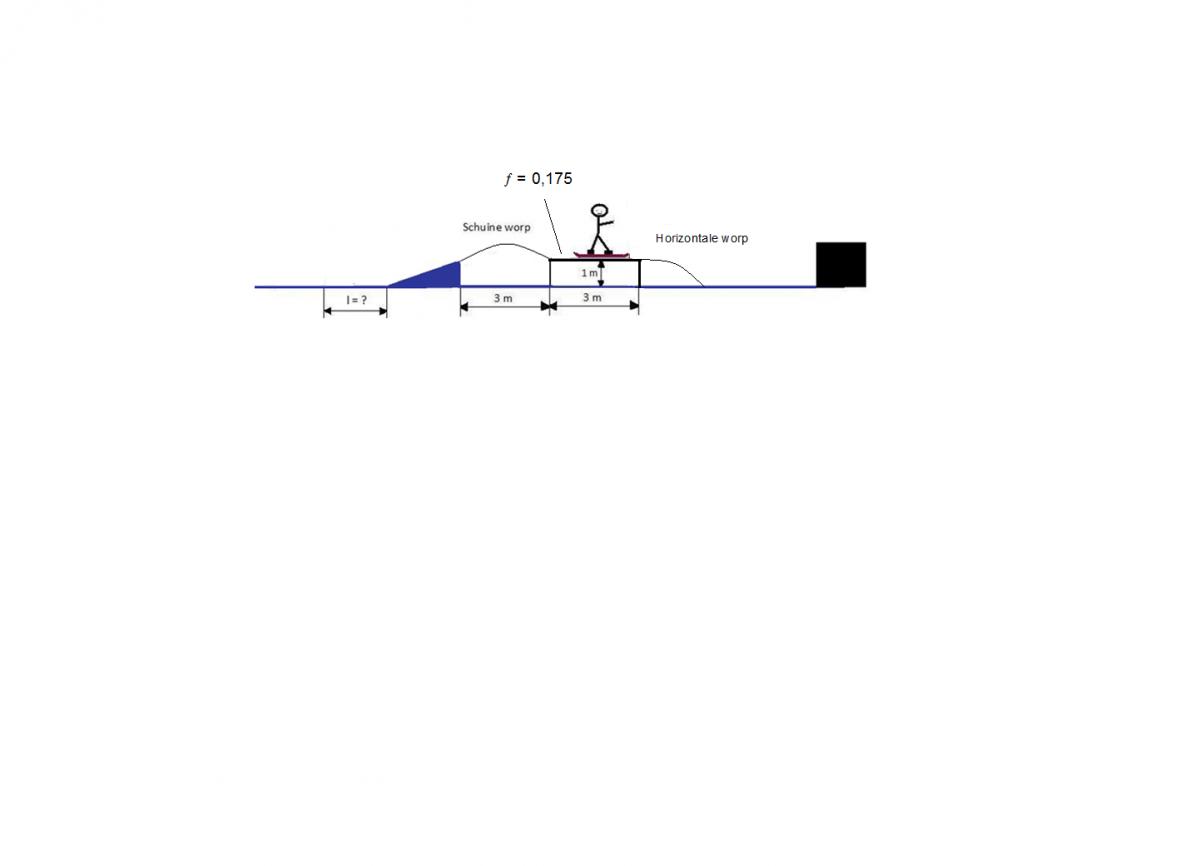
- oefening 3 444 keer bekeken
Re: vertraging bij impact
Geplaatst: za 07 mar 2015, 16:57
door Michel Uphoff
Verandert zijn verticale snelheid zodra hij de rail raakt?
Verandert zijn horizontale snelheid zodra hij de rail raakt?
Welke snelheid is er gegeven; de horizontale, de verticale, of de snelheid onder die hoek van 35 graden?
Indien de laatste, ontbind die dan eerst in een horizontale en een verticale component.
Re: vertraging bij impact
Geplaatst: za 07 mar 2015, 16:58
door Anton_v_U
Je kunt het beste de horizontale en verticale snelheid los van elkaar beschouwen. De "impact" bestaat er uit dat de snowboarder zijn verticale snelheid in korte tijd tot nul terug moet brengen. Als hij verstandig is, zakt hij door zijn knieën als hij neerkomt, want dan heeft hij meer ruimte om af te remmen (en minder kracht nodig)
Re: vertraging bij impact
Geplaatst: za 07 mar 2015, 17:32
door Willemhoeylaerts
dat is de schuine snelheid dus als je die ontbind krijg je als:
v
y = 5,6 sin35°
v
x = 5,6 cos35°
als je zegt dat hij die verticale kracht opvangt in zijn knieën, kan ik dan zeggen dat de vetraging van zijn impact verwaarloosd kan worden of niet? want na die 3 meter zal hij een horizontale worp ondergaan (zoals je ziet op de tekening). en hij land met 5,6 m/s en dan zal hij 3 meter een wrijvingskracht ondervinden wat voor een vertraging zorgt. Is dit de enige vertragingsfactor waar ik mee moet rekening houden of zijn er nog?
Anton_v_U schreef:
Je kunt het beste de horizontale en verticale snelheid los van elkaar beschouwen. De "impact" bestaat er uit dat de snowboarder zijn verticale snelheid in korte tijd tot nul terug moet brengen. Als hij verstandig is, zakt hij door zijn knieën als hij neerkomt, want dan heeft hij meer ruimte om af te remmen (en minder kracht nodig)
Michel Uphoff schreef:
Verandert zijn verticale snelheid zodra hij de rail raakt?
Verandert zijn horizontale snelheid zodra hij de rail raakt?
Welke snelheid is er gegeven; de horizontale, de verticale, of de snelheid onder die hoek van 35 graden?
Indien de laatste, ontbind die dan eerst in een horizontale en een verticale component.
Re: vertraging bij impact
Geplaatst: za 07 mar 2015, 17:39
door Michel Uphoff
Je weet nu de horizontale snelheid aan het begin van de rail.
Tijdens het glijden op de rail treedt er wrijving op, zodat zijn horizontale snelheid aan het eind van de rail minder zal zijn.
Vervolgens komt hij aan het eind van de rail in vrije val. Dan gaat de zwaartekracht een rol spelen en de verticale snelheid gaat weer omhoog. Na x seconden raakt hij de grond, en heeft hij dus ook x seconden horizontaal afgelegd, want de horizontale snelheid blijft (wrijving van de lucht buiten beschouwing gelaten) gelijk, totdat hij de grond raakt.
Lukt het je nu om het resultaat uit rekenen?
Re: vertraging bij impact
Geplaatst: za 07 mar 2015, 20:17
door Anton_v_U
Willemhoeylaerts schreef:
als je zegt dat hij die verticale kracht opvangt in zijn knieën, kan ik dan zeggen dat de vetraging van zijn impact verwaarloosd kan worden of niet?
Wat is impact? Gewoonlijk duid je daarmee het moment van een botsing aan en het heftige effect op het botsende object. Natuurkundig kun je daar niet zoveel mee want "impact" is niet meetbaar tenzij je een fysische definitie geeft die het meetbaar maakt.
In de natuurkunde gebruiken we de wetten van Newton en meetbare begrippen als snelheid vertraging, energie en impuls. In dit geval:
De verticale snelheid wordt nul en moet dus afnemen. Als je doorzakt is er een kleinere verticale vertraging nodig dan als je je lichaam stijf houdt. Dus kleinere verticale kracht op je lichaam, 2e wet van Newton. Merk op dat als je tijdens het afremmen je voeten naar beneden duwt op de grond, de grond je voeten omhoog duwt (3e wet vN) deze kracht (die is omhoog) op jouw lichaam vertraagt je beweging (want die is omlaag).
Je kunt deze verklaring kwantificeren (verzin zelf maar een rekenvoorbeeld) en dat maakt de verklaring natuurkundig acceptabel.