sciencetalk

Goedenavond,
 
Is er iets bekend over de volgende functie:
  m.a.w.: 1/2 * 2/3 * 4/5 * 6/7 * 10/11 * ....

 
Het enige vergelijkbare wat ik kan vinden is het euler product en iets over multiplicatieve functies maar dat is volgens mij toch wel wat anders. Of vergis ik mij dan?

Alvast bedankt!

Wat is de begin- en eindwaarde van p ... , of is p priem ...

https://en.wikipedia.org/wiki/Riemann_zeta_function Onder het kopje 'Euler Product Formula' wordt volgens mij uitgelegd dat dat product gelijk is aan nul, als je inderdaad alle priemgetallen meeneemt.

@Th.B: Ik snap dit niet. Bedoel je dan het specifieke geval dat s = 1? Bedoel je dat
door een aantal ‘trucjes’ uit te halen kan worden herschreven als: ?
Een product dat 0 is klinkt mij ook nogal vreemd in de oren. Dit zou moeten betekenen dat er een factor 0 voorkomt in het product, maar hoe kan zo'n factor nu ooit ontstaan?
 
@Safe: p is inderdaad een priemgetal. Als je daar grenzen aan wilt stellen: Het viel me op dat het product van alle priemgetallen onder wortel(n) vermenigvuldigd met n ongeveer het aantal priemgetallen tot n is. En dat het verschil tussen die uitkomst en het werkelijke aantal priemgetallen dan ongeveer gelijk is aan het priemgetallen tot wortel(n).

althans tot n = 100.000 lijkt het ongeveer wel te kloppen. Maar ook weer niet helemaal. En ik snap niet hoe dat nu komt dus hopelijk heeft iemand dit ooit al eens onderzocht.

 

@Th.B: Ik snap dit niet. Bedoel je dan het specifieke geval dat s = 1? Bedoel je dat
   
 

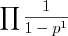
Die 1 in de exponent moet dan een -1 zijn. Kijk ook eens naar de onderste regel van het kopje (net boven 'functional equation').  
Een product van oneindig veel factoren kan best als limiet nul opleveren, zelfs als geen van de termen nul is. Kijk eens wat er gebeurt als je 1/2 heel vaak met zichzelf vermenigvuldigt.

gallo schreef: Een product dat 0 is klinkt mij ook nogal vreemd in de oren. Dit zou moeten betekenen dat er een factor 0 voorkomt in het product, maar hoe kan zo'n factor nu ooit ontstaan?

 
Elke term is kleiner dan 1, dus het convergeert naar 0 toe.

Het zijn factoren, geen termen ...

Th.B schreef: Die 1 in de exponent moet dan een -1 zijn. Kijk ook eens naar de onderste regel van het kopje (net boven 'functional equation').  
Een product van oneindig veel factoren kan best als limiet nul opleveren, zelfs als geen van de termen nul is. Kijk eens wat er gebeurt als je 1/2 heel vaak met zichzelf vermenigvuldigt.

In die onderste regel zie ik het nu inderdaad! Want (p-1)/p is gelijk aan 1 - 1/p en dat zou dan weer gelijk moeten zijn aan 1/(1-P^-s), wat het eulerproduct is (en ook nog eens 1/de riemanfunctie).

Bedankt!

  

Geen probleem