Priem tussen n2 en (n+1)2
Geplaatst: ma 28 sep 2015, 17:32
Ik zit mij af te vragen:
Waarom impliceert het feit dat het Eulerproduct min of meer gelijk is aan 1/riemanzetafunctie (1), oftewel
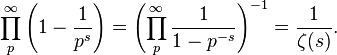
nu niet automatisch dat er tussen n2 en (n+1)2altijd een priemgetal ligt (legendre's conjecture)(2)????
Want, als ik hierover nadenk, zou je de volgende redenering op kunnen voeren:
Je kunt het aantal priemgetallen tot een X (waarvoor geldt X=n2+ 1) volgens (1) gelijk stellen aan de som van alle getallen daaronder in het kwardraat.
Je kunt het aantal priemgetallen tot een X2 (waarvoor geldt X2=(n+1)2+ 1) volgens (1) gelijk stellen aan de som van alle getallen daaronder in het kwardraat.
Aangezien er een getal van de vorm n2bij is gekomen verandert de uitkomst van de riemanzetafunctie, dus verandert de uitkomst van het Eulerproduct, dus wordt er tenminste 1 nieuw priemgetal aan dat nieuwe Eulerproduct toegevoegd. Van dat priemgetal is bekend dat het tussen n2en (n+1)2 ligt.
Zit de fout hem nu in het feit dat (1) alleen geldig is in het oneindige? en niet voor een heel groot getal X of X2?
Zo ja, wat is dan in hemelsnaam de waarde van (1) wanneer het feitelijk nooit waar is, behalve voor een oneindig groot getal (dat dus eigenlijk niet bestaat).
Waarom impliceert het feit dat het Eulerproduct min of meer gelijk is aan 1/riemanzetafunctie (1), oftewel
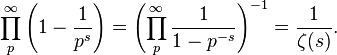
nu niet automatisch dat er tussen n2 en (n+1)2altijd een priemgetal ligt (legendre's conjecture)(2)????
Want, als ik hierover nadenk, zou je de volgende redenering op kunnen voeren:
Je kunt het aantal priemgetallen tot een X (waarvoor geldt X=n2+ 1) volgens (1) gelijk stellen aan de som van alle getallen daaronder in het kwardraat.
Je kunt het aantal priemgetallen tot een X2 (waarvoor geldt X2=(n+1)2+ 1) volgens (1) gelijk stellen aan de som van alle getallen daaronder in het kwardraat.
Aangezien er een getal van de vorm n2bij is gekomen verandert de uitkomst van de riemanzetafunctie, dus verandert de uitkomst van het Eulerproduct, dus wordt er tenminste 1 nieuw priemgetal aan dat nieuwe Eulerproduct toegevoegd. Van dat priemgetal is bekend dat het tussen n2en (n+1)2 ligt.
Zit de fout hem nu in het feit dat (1) alleen geldig is in het oneindige? en niet voor een heel groot getal X of X2?
Zo ja, wat is dan in hemelsnaam de waarde van (1) wanneer het feitelijk nooit waar is, behalve voor een oneindig groot getal (dat dus eigenlijk niet bestaat).