1 van 1
DSP
Geplaatst: vr 02 dec 2016, 23:17
door ukster
Ik wil een signaal onderzoeken op betrouwbare frequentiecomponenten t/m 5,11 MHz met een resolutie R=10KHz.
a. Hoeveel Samples N moeten er minimaal genomen worden.
b. Windowtijd Tw.
c. Wat is de minimale bemonsteringsfrequentie fb.
Re: DSP
Geplaatst: za 03 dec 2016, 02:12
door Benm
Praktisch lastig: Je zou met een 10,22 MHz samplerate af kunnen indien je signaal geen componenten boven 5,11 MHz bevat, of je een oneindig steil anti-aliasing filter hebt (theorie).
Voor de overige vragen is het van belang wat je wilt weten: je heeft aan een frequentie-resolutie van 10 kHz te willen, maar je moet ook de amplitude-resolutie weten om te kunnen berekenen hoeveel samples je nodig hebt voor een gegeven window time of vice versa.
Re: DSP
Geplaatst: za 03 dec 2016, 13:35
door ukster
Mee eens, (NYQUIST/SHANNON) schrijft voor dat Aliasing voorkomen kan worden door er voor te zorgen dat de bemonsteringsfrequentie fb>2fmax
Dit schept de mogelijkheid voor een vervormingsvrije detectie van signalen (althans wat betreft de frequentiecomponenten)
Maar wat betreft het minimaal aantal te nemen samples stel jij dat dit ook te maken heeft met de Amplitude Resolutie.
Volgens mij is dat niet zo,omdat dit alleen te maken heeft met het aantal kwantiseringsnivo's waarmee een analoog signaal in discrete niveaus kan worden omgezet (PAM) om daarna digitaal gecodeerd te worden (PCM).
Alleen tijd(parameters) leggen de relatie met frequenties in het te onderzoeken frequentiespectrum.
Re: DSP
Geplaatst: za 03 dec 2016, 14:08
door ukster
Dan denk ik aan: Aantal samples N, Samplenummer xn=0,1,2,.....),Samplefrequentie fb,Sampletijd Tb, Windowtijd Tw
En door hierop de Fouriertransformatie (FT) los te laten kan hieruit de aanwezige frequentiecomponenten in het signaalfrequentiespectrum bekend worden.
En omdat een computer alleen met discrete waarden overweg kan,moeten de gesampelde waarden via een DFT /FFT worden geprocessed.
Het lijkt mij dat alle eigenschappen in het frequentiespectrum zoals max betrouwbare frequentiecomponent en resolutie direct gelinkt zijn aan de parameters in het te meten tijdvenster (window)
Re: DSP
Geplaatst: za 03 dec 2016, 14:25
door Benm
De grootte van het window is in ieder geval bepalend voor de laagste frequentie die je nog kunt analyseren. Als je bijvoorbeeld batches van 1000 samples zou processen met een sample rate van 10 MHz kun je signalen trager dan ~20 kHz niet correct meten (er moet een complete sinus van het signaal in het window vallen).
Verder is de resolutie van belang. Stel dat je 16 bits samples neemt en het signaal opknipt in 32 (gelijke) frequentiebanden, dan houd je per band pakweg 11 bits over. Meestal is dat niet zo'n bezwaar als het om visualisatie gaat, maar als je extreem veel banden gebruikt, hoge nauwkeurigheid nodig hebt, of met weinig (bijv 8) bits kunt sampelen speelt het een rol.
Re: DSP
Geplaatst: za 03 dec 2016, 14:26
door ukster
Overigens is het ook niet zo dat als er voldaan wordt aan het bemonsteringstheorema van Nyquist (voldoende samples) of door het toepassen van een anti Aliasing filter aan de ingang, we van de alle vervorming in het te onderzoeken frequentiespectrum af zouden zijn.
Een ideaal window heeft een rechthoekige vorm (rectangular) en in de repetitieve mode geeft dat een sincspectrum met heel veel zijlussen die zich diep in beide richtingen in het spectrum uitstrekken waardoor dichtbijgelegen signaalfrequentiecomponenten misschien niet gedetecteerd worden.(Sincvervuiling)
Dan moet je aan zo'n window gaan sleutelen en deze een aangepaste vorm geven, waardoor misschien het aantal zijlussen afneemt, maar waardoor de breedte van de hoofd(detectie)lus toeneemt.
Re: DSP
Geplaatst: za 03 dec 2016, 14:34
door ukster
Dat als ik jouw goed begrijp moet dus de 1e harmonische (basisgolf) precies in het window passen.
maar dan is de windowtijd bekend.
de afstand tussen alle frequentiepaaltjes (resolutie) in het te onderzoeken spectrum is 10kHz.
de 1e harmonische is dus 10kHz, de 2e harmonische 20kHz etc
periodetijd 1e harmonische T=1/f= 100us, dus dan moet de windowtijd Tw=100us zijn, waarin alle N samples worden genomen.
Re: DSP
Geplaatst: za 03 dec 2016, 15:15
door ukster
Als ik na sampling een betrouwbare frequentiecomponenten wil aantonen tot en met fmax= 5,11MHz met een resolutie van R=10kHZ, dan zitten er dus fmax/R = 511 paaltjes(harmonischen) is het spectrum, dus kmax=511 (k is het harmonischennummer)
k=512 is de spiegelfrequentie.
Volgens Nyquist is dan de gespiegelde helft van de harmonischencomponenten vals, dus k=513 t/m k=1023.
k=1024 is weer een spiegel waar voorbij het gehele spectrum zich weer herhaald.
Relateer ik dit aan het aantal te nemen samples N,rekening houdend met Nyquist, kom ik tot de conclusie dat kmax=N/2-1, dus N=2(kmax+1)
dus N=1024 samples in een windowtijd Tw=100us
Dit betekent een Sampletijd vanTb=Tw/N = 0,9765625 us
Samplefrequentie fb=1/Tb= 10,24 MHz (dit klopt met het theorema van Nyquist)
Re: DSP
Geplaatst: za 03 dec 2016, 17:34
door Benm
Dat lijkt me wel te kloppen inderdaad. Praktisch gezien zou ik het aanzienlijk ruimer nemen en die ADC op 16 MHz oid klokken, wellicht nog wel wat meer. Chipset bedoeld voor een digitale scope lijkt me het meest handig, al is de resolutie daarvan soms niet al te best.
Re: DSP
Geplaatst: za 03 dec 2016, 18:01
door ukster
Ja, ik begrijp dat het altijd een macht van 2 is. (4-8-16-32......1024-2048 etc.)
Heet dit niet oversampling?
Om de rekencapaciteit maximaal te benutten zou je dan twee of meer informatiekanalen tegelijkertijd kunnen bemonsteren.
(Samples om en om)
Het snelle rekenwerk (FFT) wordt praktisch hardwarematig uitgevoerd middels Butterfly configuraties.
In een aantal rekenslagen wordt uit de genomen tijdsamples de aanwezige frequenties met bijbehorende amplitude berekend.
Handig bij radar- en sonarsystemen of digitale Filtering
Re: DSP
Geplaatst: za 03 dec 2016, 18:35
door ukster
voorbeeld van een 16 punts FFT (N=16) Butterfly, DIF(Decimation in Frequency)
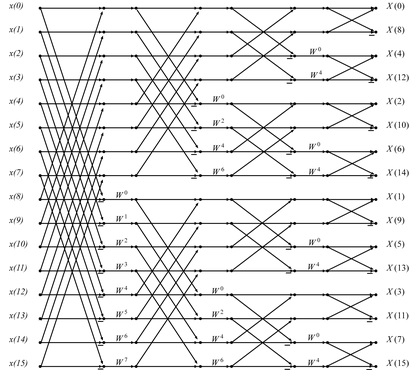
- 16 punts (N=16) FFT Butterfly 851 keer bekeken
Re: DSP
Geplaatst: zo 04 dec 2016, 02:09
door Benm
Oversampling inderdaad. Dit hoeft niet per se een 2-macht boven de benodigde samplerate te zijn, al wordt het vaak wel zo toegepast (met 4x oversampling krijg je na rekenwerk een extra bit resolutie etc).
Het is natuurlijk de vraag of dat aansluit bij je eisen. Als je ergens een '100MHz' label op wilt plakken moet je sampelen met 200 MS/s of beter. Er is niets dat je let om zo'n 200 MS/s ADC te gebruiken om een signaal tot 5 MHz te gebruiken. Dat is op zich 40x 'overkill' maar levert je potentieel wel 2 a 3 bit extra resolutie op... handig als je die chip voorhanden hebt of het ding gewoon heel betaalbaar is.
Re: DSP
Geplaatst: zo 04 dec 2016, 10:22
door ukster
Oke Benm, dank voor je zinvolle bijdrage
ik ga ermee aan de slag.