1 van 2
Druk op buitenoppervlak halve cilinder
Geplaatst: wo 12 dec 2018, 11:45
door woodynederl
Voor een project moet ik de druk berekenen die wordt gegeven door een tape op een cilindervormig vlak. In de bijlage is de situatie geschetst. Hoe zou ik dit het beste kunnen aanpakken?
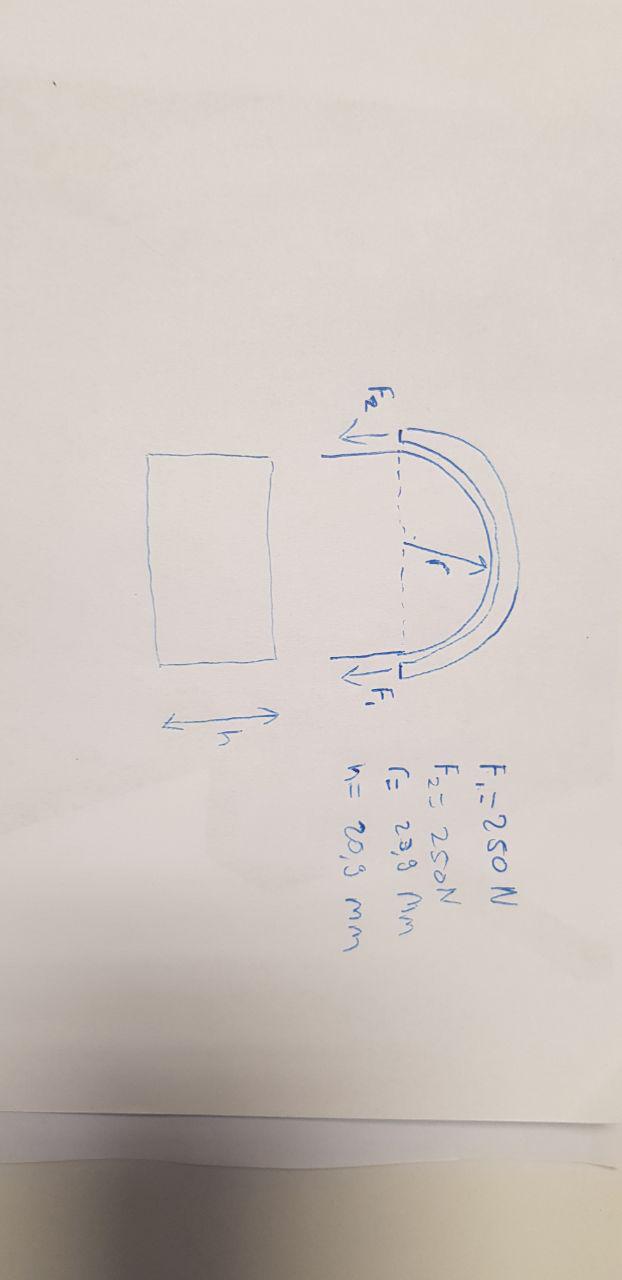
- photo_2018-12-12_11-42-50 1603 keer bekeken
Re: Druk op buitenoppervlak halve cilinder
Geplaatst: wo 12 dec 2018, 12:00
door dannypje
Welke totale kracht wordt er uitgeoefend ?
Wat is de definitie van druk ?
Re: Druk op buitenoppervlak halve cilinder
Geplaatst: wo 12 dec 2018, 15:33
door woodynederl
De totale kracht bedraagt 500N. Ik begrijp je vraag omtrent druk niet helemaal? Definitie van druk, bedoel je daar het volgende mee: P = F/A? MPa, N/mm^2?
dannypje schreef:
Welke totale kracht wordt er uitgeoefend ?
Wat is de definitie van druk ?
Re: Druk op buitenoppervlak halve cilinder
Geplaatst: wo 12 dec 2018, 16:15
door dannypje
woodynederl schreef:
De totale kracht bedraagt 500N. Ik begrijp je vraag omtrent druk niet helemaal? Definitie van druk, bedoel je daar het volgende mee: P = F/A? MPa, N/mm^2?
MPa en N/mm^2 zijn eenheden van druk (en beiden niet echt SI. wat is de SI eenheid van druk ?). De eerste is de definitie: kracht per oppervlakte , nu ja, niet P=F/A maar p=F/A.
Je weet dus nu de totale kracht, en je kent de afmetingen van de tape, dus je kan de oppervlakte berekenen waarop die kracht werkt.
Re: Druk op buitenoppervlak halve cilinder
Geplaatst: wo 12 dec 2018, 16:41
door woodynederl
SI-eenheid is Pa. Is p=F/A niet alleen te gebruiken voor een vlak oppervlak? Zal de loodrechte component (en dus de druk op het cilinderoppervlak) niet afnemen naar mate je verder verwijderd bent van "het midden"?
dannypje schreef:
MPa en N/mm^2 zijn eenheden van druk (en beiden niet echt SI. wat is de SI eenheid van druk ?). De eerste is de definitie: kracht per oppervlakte , nu ja, niet P=F/A maar p=F/A.
Je weet dus nu de totale kracht, en je kent de afmetingen van de tape, dus je kan de oppervlakte berekenen waarop die kracht werkt.
Re: Druk op buitenoppervlak halve cilinder
Geplaatst: do 13 dec 2018, 09:45
door Xilvo
Als je eventuele zwaartekracht verwaarloost/niet meerekent en als je aanneemt dat er geen wrijving tussen tape en cilinderoppervlak is (ze kunnen perfect over elkaar heen glijden), dan is die loodrechte component op het oppervlak overal gelijk. Er ís ook alleen maar een loodrechte component, voor een dwarscomponent zou juist wrijving nodig zijn.
Kijk ook eens naar dit draadje, het heeft overeenkomsten met dit vraagstuk:
https://sciencetalk.nl/forum/index.php/topic/207092-rapunzel/page-4
Re: Druk op buitenoppervlak halve cilinder
Geplaatst: do 13 dec 2018, 11:42
door woodynederl
Als we zwaartekracht en wrijving weglaten zou dit dus de oplossing moeten zijn:
A=π*r*h -> π*0.0239*0.0209=0.001568 m2
p=F/A -> 500/0.001568≈0.318877 MPa
Xilvo schreef:
Als je eventuele zwaartekracht verwaarloost/niet meerekent en als je aanneemt dat er geen wrijving tussen tape en cilinderoppervlak is (ze kunnen perfect over elkaar heen glijden), dan is die loodrechte component op het oppervlak overal gelijk. Er ís ook alleen maar een loodrechte component, voor een dwarscomponent zou juist wrijving nodig zijn.
Kijk ook eens naar dit draadje, het heeft overeenkomsten met dit vraagstuk:
https://sciencetalk.nl/forum/index.php/topic/207092-rapunzel/page-4
Re: Druk op buitenoppervlak halve cilinder
Geplaatst: do 13 dec 2018, 12:14
door Xilvo
Nee, dat is nog niet goed. Kijk nog eens naar bericht #51 in het andere draadje (dat is niet het enige bericht waar je wat mee kunt maar omdat ik dat zelf schreef vind ik het het makkelijkst daar over de praten). Wat is s, wat is r, wat is x?
Denk verder nog eens wat de spankracht s in het tape werkelijk is.
Re: Druk op buitenoppervlak halve cilinder
Geplaatst: do 13 dec 2018, 13:24
door woodynederl
Als je de tape op een willekeurige plek doorknipt zal de tegenwerkende kracht altijd 250N zijn, aangezien de tape niet in beweging is.
Dus:
s=250N
r=0,0239m

-> 500*0.0239=Δx*250 -> Δx=0.0478 (uiteindelijk dus "gewoon" 2*r)
Echter begrijp ik nu nog niet hoe ik verder kom, aangezien voorgaande post niet correct was.
Xilvo schreef:
Nee, dat is nog niet goed. Kijk nog eens naar bericht #51 in het andere draadje (dat is niet het enige bericht waar je wat mee kunt maar omdat ik dat zelf schreef vind ik het het makkelijkst daar over de praten). Wat is s, wat is r, wat is x?
Denk verder nog eens wat de spankracht s in het tape werkelijk is.
Re: Druk op buitenoppervlak halve cilinder
Geplaatst: do 13 dec 2018, 13:38
door Xilvo
Weer een stap verder/ Maar er staat s/r, niet s*r. En waarom gebruik je nu toch weer 500 N, niet 250 N?
Bedenk dat dx langs het oppervlak is, in de langsrichting van het tape.
De druk is dan de kracht ΔF gedeeld door het oppervlak ΔA=h.Δx.
Overigens is het bij dit soort sommetjes altijd handig een ruwe schatting te maken, zodat je het herkent als er onzin uit je berekening komt.
Het totale 'horizontale' oppervlak (ik heb de tekening in gedachten 90 graden linksom gedraaid) is 2.r.h; de totale kracht naar beneden 2.250 N (nu wèl maal twee!). Hiermee kun je uitrekenen in welke grootte-orde je antwoord moet liggen.
Re: Druk op buitenoppervlak halve cilinder
Geplaatst: do 13 dec 2018, 13:48
door Xilvo
Ik las je berichtje niet goed, zie ik. Maar ΔF/Δx kun je nog niet invullen, die wil je juist weten/berekenen om de druk te weten te komen. Zie berichtje hierboven.
Re: Druk op buitenoppervlak halve cilinder
Geplaatst: do 13 dec 2018, 14:15
door woodynederl
Ruwe schatting:
(2*250)/(2*0.0239*0.0209) = 500490 Pa = 0,5 MPa
Hier begrijp ik niet hoezo je 2*r*h gebruikt?
De oppervlakte van een cilinder (zonder voet en kruin) is toch: 2*π*r*h (in ons geval: π*r*h, aangezien het een halve cilinder is)?
Doorgaand op bericht #10:
ΔA=h*Δx
ΔA(π*0.0239*0.0209)/h(0.0209)=Δx(0.075) -> hier kan je dan toch net zo goed π*r doen?
Bovenstaand zal wel niet kloppen aangezien je niet met iets gaat vermenigvuldigen om daarna door hetzelfde te delen.
Het blijkt dat ik nog steeds het spoor bijster ben.
Re: Druk op buitenoppervlak halve cilinder
Geplaatst: do 13 dec 2018, 14:23
door Xilvo
"Hier begrijp ik niet hoezo je 2*r*h gebruikt? "
Een vlak oppervlak, voor die ruwe schatting, dat is dus niet de èchte berekening.
Als je ΔF/Δx weet (uit s/r), en ΔA=h*Δx, dan kun je toch die druk berekenen?
Re: Druk op buitenoppervlak halve cilinder
Geplaatst: do 13 dec 2018, 14:35
door woodynederl
Duidelijk, dus ruwe schatting: 0,5 MPa.
s/r -> 250/0,0239=10460
Δx=2*r=0,075
10460*0,075=784,5
784,5/(π*0,0239*0,0209)≈500171 Pa = 0,5 MPa
Re: Druk op buitenoppervlak halve cilinder
Geplaatst: do 13 dec 2018, 15:13
door Xilvo
Eigenlijk moet je Δx heel klein kiezen, dx, maar omdat de kracht overal even groot is maakt het hier niet uit.
En het echte antwoord blijkt toevallig gelijk te zijn aan wat de ruwe schatting oplevert.
