sciencetalk

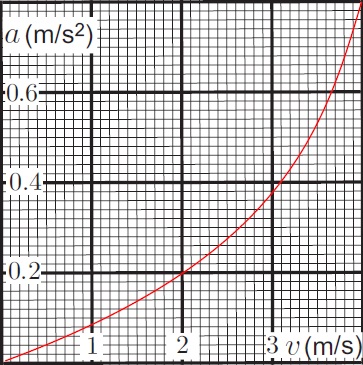
De versnelling van een boot hangt af van zijn snelheid als getoond in de grafiek.
De boot krijgt de beginsnelheid v₀=4m/s
Wat is de totale afgelegde afstand tot de boot bijna tot rust is gekomen?
Dit is wat ik kan bedenken:
ds=vdt
dv=adt
dt=dv/a
ds=(v/a)dv
Hoe komt men nu aan het antwoord 39m?

Waar komt deze vraag vandaan?
 
Ik zou de kromme proberen te fitten met een polynoom en vervolgens numeriek integreren. Maar ik vermoed dat dat niet de bedoeling is?

Bundel vragen 'problems on kinematics' wel antwoorden maar geen uitwerkingen
ds=(v/a)dv
s= :SIGMA: (v/a)Δv handmatig in de grafiek misschien?
of inderdaad s= greek036.gif (v/a)dv numeriek (curve fit)
Alleen het antwoord 39m is gegeven

Grafiek gefit (4e-graads polynoom) vervolgens, nogal primitief, geïntegreerd in Excel, dt = 0,2 s.
 
Snelheid wil niet echt nul worden omdat de vertraging ook vrijwel nul wordt.
Bij v≈0.001 is de afstand dan 40,12 m.

Aha.. op die manier dus

Maar of dat de bedoeling was... 

Ik ga ervan uit dat dit toch de bedoeling was.....anders is het niet te doen toch?

Mocht ik ineens nog een geniale ingeving krijgen dan laat ik het weten. 

Haha.. Oke

Met ds=(v/a)dv, uit je eerste post (weer dezelfde fit voor a gebruikt) en dv=0,0.2, krijg ik een afstand van 40,26 m.