1 van 1
Snelheid berekenen oliedemper
Geplaatst: vr 27 sep 2019, 10:14
door itsBart
Ik heb oliedemper die door een bepaalde kracht in wil schuiven maar wordt gedempt door de dempingskracht (zie VLS). Nu wil ik graag berekenen hoe snel hij in zal schuiven.
Het VLS is als volgt:
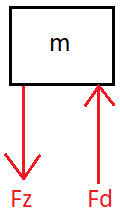
- VLS
- Demping 3847 keer bekeken
Toepassen van de Tweede wet van Newton geeft:
∑Fy = m⋅a
Fz - Fd = m⋅a
m⋅g - K⋅v = m⋅a
m⋅g - K⋅v = m⋅(dv/dt)
g - K⋅v/m = dv/dt
homogeen maken:
g - K⋅v/m = (v(t+Δt) - v(t))/Δt
v(t+Δt) = v(t) + g⋅Δt - K⋅v(t)⋅Δt/m
Deze differentievergelijking heb ik in Excel gezet. Ik heb een waarde voor K aangenomen, en krijg de volgende grafiek:
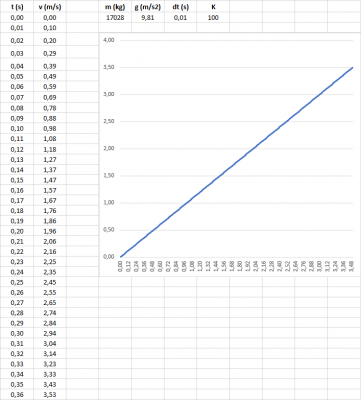
- Grafiek
Ik neem aan dat ik iets vergeten ben of verkeerd doe, aangezien de snelheid gedempt hoort te worden i.p.v. te worden verhoogd. Kan iemand mij hiermee helpen?
Daarnaast vroeg ik mij af hoe ik de dempingscoëfficiënt K kan bepalen. Om exact te zijn betreft het een hydraulische cilinder die in drukloze toestand is gezet. De oppervlakte van de boring bedraagt 2,5E-02 m², de oppervlakte van de opening waar olie de cilinder verlaat bedraagt 7,9E-05 m². De dichtheid van de olie is 900 kg/m³.
Bij voorbaat dank.
Re: Snelheid berekenen oliedemper
Geplaatst: vr 27 sep 2019, 11:00
door Xilvo
Je doet niets fout. Maar de snelheid verandert pas niet meer als g - K.vt / m=0.
Dan is de snelheid 1670 m/s. Je moet dus langer door gaan (bijvoorbeeld dt groter kiezen).
Re: Snelheid berekenen oliedemper
Geplaatst: vr 27 sep 2019, 11:20
door itsBart
Dat klopt inderdaad. Dankjewel.
Nu vraag ik mij echter nog af of het niet zo moet zijn dat de snelheid hoog begint en dan afneemt, in tegenstelling tot de huidige resultaten. Misschien heb ik het inzichtelijk mis, maar volgens mij moet de demper op het moment dat de last wordt uitgeoefend eerst heel snel willen bewegen en dat dit door de dempingskracht van de olie door de uitloop meteen afremt.
Re: Snelheid berekenen oliedemper
Geplaatst: vr 27 sep 2019, 11:31
door Xilvo
Die beginsnelheid kun je zelf kiezen, en die is bij jou blijkbaar nul (waarde in eerste cel onder "v (m/s)")
Kies je een snelheid groter dan 1670 m/s, dan daalt die en nadert 1670 dan asymptotisch van boven.
Re: Snelheid berekenen oliedemper
Geplaatst: vr 27 sep 2019, 11:39
door ukster
zoiets?
K=2000
m=17028
v(0)=100m/s
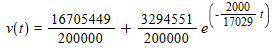
- snelheid 3823 keer bekeken
- oliedemper 3823 keer bekeken
Re: Snelheid berekenen oliedemper
Geplaatst: vr 27 sep 2019, 11:49
door itsBart
Xilvo schreef: ↑vr 27 sep 2019, 11:31
Die beginsnelheid kun je zelf kiezen, en die is bij jou blijkbaar nul (waarde in eerste cel onder "v (m/s)")
Kies je een snelheid groter dan 1670 m/s, dan daalt die en nadert 1670 dan asymptotisch van boven.
Daarmee heb ik inderdaad de grafiek die ik in gedachte had. Dankjewel!
ukster schreef: ↑vr 27 sep 2019, 11:39
zoiets?
K=2000
m=17028
v(0)=100m/s
snelheid.png
oliedemper.png
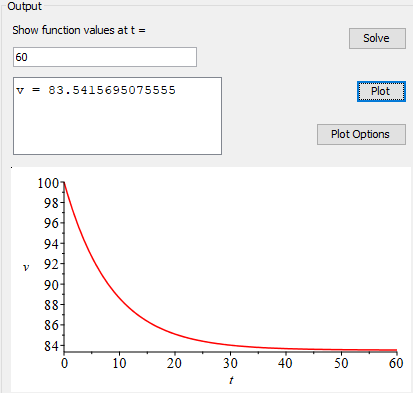
Dit ziet er ook goed uit. Gebruik jij een andere functie, en zo ja, wat is de herkomst hiervan? Dankjewel.
Nu rest mij alleen nog een definitieve K te bepalen. De snelheden lijken nu erg hoog, ik hoop dat die uiteindelijk lager ligt

Re: Snelheid berekenen oliedemper
Geplaatst: vr 27 sep 2019, 11:54
door itsBart
Ik ben eigenlijk op zoek naar een resultaat die deze nadert:
(dit betekent dat ik een K nodig heb van ~200.000)
Ik hoop dat iemand mij nog kan helpen met de bepaling hiervan.
Re: Snelheid berekenen oliedemper
Geplaatst: vr 27 sep 2019, 11:59
door ukster
K=200000
v(0)=100m/s
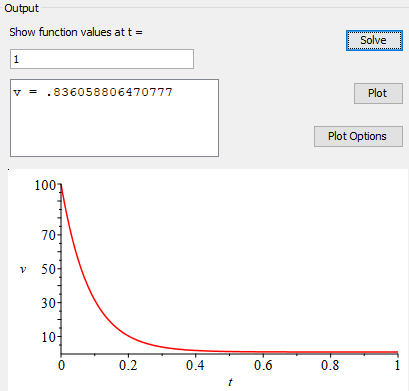
- oliedemper 3809 keer bekeken
Re: Snelheid berekenen oliedemper
Geplaatst: vr 27 sep 2019, 11:59
door Xilvo
Het is mij niet duidelijk welke eis je stelt.
Als dat een bepaalde eindsnelheid is, dan kun je K halen uit g - K.veind / m=0
Re: Snelheid berekenen oliedemper
Geplaatst: vr 27 sep 2019, 12:01
door itsBart
Ik begrijp dat ik zo de K kan berekenen. Echter wil ik graag weten hoe mijn demper eruit moet zien om die K te realiseren, indien mogelijk. Constructiegewijs, dus.
Mijn excuses voor de onduidelijkheid.
Re: Snelheid berekenen oliedemper
Geplaatst: vr 27 sep 2019, 12:10
door Xilvo
itsBart schreef: ↑vr 27 sep 2019, 12:01
Echter wil ik graag weten hoe mijn demper eruit moet zien om die K te realiseren, indien mogelijk.
Dààr kan ik weinig over zeggen, misschien dat er andere forumleden zijn die daar kennis over hebben.
Ik weet zelfs niet of bij een demper als een schokbreker van een auto de kracht wel recht evenredig is met de snelheid.
Die kracht zou bijvoorbeeld ook evenredig kunnen zijn met het kwadraat van de snelheid, zoals min of meer het geval is bij een voorwerp dat door een gas of vloeistof beweegt.
Waar gaat het over? Die (grote) massa van 17028 kg doet vermoeden dat het om een praktisch probleem gaat.
Re: Snelheid berekenen oliedemper
Geplaatst: vr 27 sep 2019, 12:16
door itsBart
Het gaat over een groot platform die met cilinders kan worden gesloten (en geopend), en in geopende toestand op het water ligt en in een 'vaanstand' wordt gezet (zonder druk op de cilinders) zodat hij op de golven meedeint.
Wanneer het platform wordt opgetild door een golf die vervolgens snel weer verdwijnt, valt het platform naar onderen. Ik wilde graag berekenen in hoeverre de cilinders de snelheid van het vallen dempen.
Re: Snelheid berekenen oliedemper
Geplaatst: vr 27 sep 2019, 12:32
door Xilvo
Ah, dat roterende platform. Dat heb ik eerder gezien, inderdaad.
Dat het roteert en niet lineair beweegt verandert de zaak een beetje, maar niet principieel.
Ik hoop dat iemand anders je informatie kan verstrekken over de praktische aspecten van dempers.
Bedenk verder dat een demper bewegingsenergie omzet in warmte, die warmte moet wel afgevoerd kunnen worden.
In het hypothetisch geval hierboven, met een (waanzinnig hoge) beginsnelheid van 1670 m/s, komt dat bij jouw massa neer op 2,4E10 J. Daar kun je een heel grote demper mee smelten

Succes!
Re: Snelheid berekenen oliedemper
Geplaatst: vr 27 sep 2019, 12:38
door itsBart
Gelukkig is dat slechts theoretisch het geval. Golven hebben een beperkte helling en verplaatsen zich lang niet snel genoeg om het platform vrij te laten vallen ^^. Zeker gezien het platform alleen mag worden gebruikt bij een zwakke deining.
Nogmaals bedankt voor je hulp.