1 van 2
DV
Geplaatst: za 10 jul 2021, 16:14
door ukster
Hoe werkt hier de scheiding van variabelen om vervolgens de oplossing (in impliciet format) van de DV te vinden?
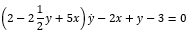
- Scheiding van variabelen 2175 keer bekeken
Re: DV
Geplaatst: za 10 jul 2021, 20:54
door Cookz
Waar is de afgeleide naar de 2 variabele?
Anders zou ik zeggen niet, en heb je gewoon een eerste graad DV met x als parameter.
Re: DV
Geplaatst: za 10 jul 2021, 21:09
door Cookz
2de variabele*
Re: DV
Geplaatst: za 10 jul 2021, 21:53
door ukster
Het schijnt dat een goedgekozen substitutie variabelenscheiding mogelijk maakt. De oplossing volgt dan uit integratie van linkerlid en rechterlid, waarna door backsubstitutie de oplossingvergelijking van de DV volgt.
(uitgedrukt in x en y)
Re: DV
Geplaatst: zo 11 jul 2021, 10:11
door tempelier
De stukken in x en y zijn veelvouden van elkaar.
Maak dat ze ook door een geschikte vermenigvuldiging het lukt dan wel.
Re: DV
Geplaatst: zo 11 jul 2021, 11:20
door ukster
Oke! Jouw voorgestelde substitutie maakt in gereduceerde vorm de scheiding van variabelen mogelijk.
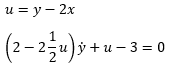
- substitutie 1983 keer bekeken
Re: DV
Geplaatst: zo 11 jul 2021, 11:28
door Professor Puntje
En verder...
Re: DV
Geplaatst: zo 11 jul 2021, 11:36
door tempelier
Ik had begrepen dat er niet meer gevraagd werd.
Re: DV
Geplaatst: zo 11 jul 2021, 11:48
door Professor Puntje
@ Tempelier
ukster schreef: ↑za 10 jul 2021, 16:14
(...) om vervolgens de oplossing (in impliciet format) van de DV te vinden?
Re: DV
Geplaatst: zo 11 jul 2021, 12:28
door tempelier
Professor Puntje schreef: ↑zo 11 jul 2021, 11:48
@ Tempelier
ukster schreef: ↑za 10 jul 2021, 16:14
(...) om vervolgens de oplossing (in impliciet format) van de DV te vinden?
Mij lijkt het dat hij dat zelf kan, of is het bedoeld dat wij moeten laten zien dat we het ook kunnen?
Re: DV
Geplaatst: zo 11 jul 2021, 12:33
door Professor Puntje
Mogelijk mis ik iets, maar ik zie nog niet hoe je dat doet.
Re: DV
Geplaatst: zo 11 jul 2021, 12:58
door ukster
Ik ga een poging doen dit met de hand op te lossen..
Re: DV
Geplaatst: zo 11 jul 2021, 12:59
door Professor Puntje
Mooi!

Re: DV
Geplaatst: zo 11 jul 2021, 13:00
door tempelier
Maak eerst van y' dy/dx.
Herschrijft naar f(x,y)dy= g(x,y)dx
Vooer dan de substitutie uit. u=y-2x enz.
Re: DV
Geplaatst: zo 11 jul 2021, 15:41
door ukster