1 van 3
vergelijkingen
Geplaatst: za 31 jul 2021, 13:37
door ukster
Er zijn 3 oplossingen van dit systeem vergelijkingen!
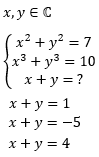
- oplossingen 4190 keer bekeken
Hoe kan ik deze oplossingen bevestigen? Ik bedoel, is er een manier om de eerste en tweede vergelijking te controleren?
Re: vergelijkingen
Geplaatst: za 31 jul 2021, 14:11
door Xilvo
Terug invullen, bijvoorbeeld voor
\(x+y=1\)
\(y=1-x\)
\(x^2+(1-x^2)-7=0\)
\(x^2-x-3=0\)
\(x_1=-1,30278\)
\(x_2=2,30278\)
y weer uitrekenen met
\(y=1-x\) en invullen in
\(x^3+y^3\) en zien dat er inderdaad 10 uitkomt.
Re: vergelijkingen
Geplaatst: za 31 jul 2021, 15:54
door ukster
x+y=1 (x,y reëel)
x+y=-5 (x,y complex)
x+y=4 (x,y complex voor x
3+y
3=10)
x+y=4 (x,y reëel voor x
2+y
2=7)
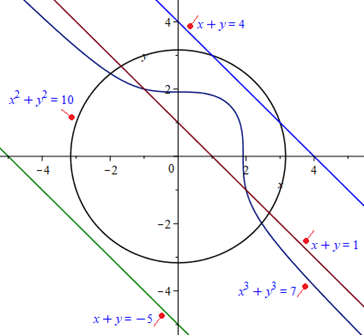
- graph 4144 keer bekeken
Re: vergelijkingen
Geplaatst: za 31 jul 2021, 17:23
door Xilvo
Ik had het natuurlijk voor de andere twee gevallen ook even moeten controleren, die antwoorden konden niet reëel zijn.
Dit zijn de snijpunten:
x+y=1
x=-1,3028 y=2,3028)
x=2,3028 y=-1,3028
x+y=-5
x=-2,5 - 1,6583 i, y=-2,5 + 1,6583 i
x=-2,5 + 1,6583 i, y=-2,5 - 1,6583 i
x+y=4
x=2 - 0,7071 i, y=2 + 0,7071 i)
x=2 + 0,7071 i, y=2 - 0,7071 i
N.B. De cirkel in jouw afbeelding moet natuurlijk straal 7 hebben.
Re: vergelijkingen
Geplaatst: za 31 jul 2021, 17:35
door ukster
allemaal slordigheidjes..
Dit is beter!
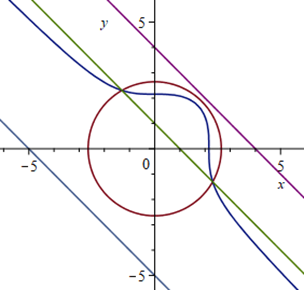
- graph 4116 keer bekeken
Re: vergelijkingen
Geplaatst: za 31 jul 2021, 20:18
door ukster
En wat zijn nu de oplossingen voor x+y ?
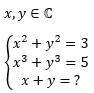
- stelsel vergelijkingen 4072 keer bekeken
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 11:45
door Xilvo
ukster schreef: ↑za 31 jul 2021, 20:18
En wat zijn nu de oplossingen voor x+y ?
-3,4495 1,4495 en 2. Numeriek gevonden.
Is het zomaar wiskunde om de wiskunde of heeft het ook een betekenis/toepassing?
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 13:03
door ukster
Hou het op wiskunde om de wiskunde. Voor mij de nodige hersenactiviteit, en 't zit zo vernuftig in elkaar. Ik heb het altijd als prettig ervaren als de 'dingen' kloppen, dat de wetmatigheden, zeg maar, ook echt wetmatigheden zijn en waar niet vervolgens 63 uitzonderingen op zijn. kennis nemen van de vele wiskundige ‘trucjes’ en oplossingsstrategieën om een bepaald probleem aan te pakken. Blijft interessant!
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 13:05
door tempelier
Dat heb ik ook gevonden.
Ik denk dat we iets over de kop zien die 2 lijkt precies 2 te zijn.
Dat duidt er op dat er misschien ergens een truc is om (x+y) rechtstreeks te vinden.
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 13:10
door ukster
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 13:25
door Xilvo
Mooi! Zelf gevonden?
Ik kan me (nog) geen voorstelling maken bij zo'n complex snijpunt.
De x-as kan je uitbreiden tot een complex vlak met de imaginaire richting loodrecht op het papier. Zeg maar de z-richting.
Idem voor de y-as. Maar is dat diezelfde z-richting, waardoor het een driedimensionaal probleem wordt?
Of is dat een andere dimensie, wat het een vierdimensionaal vraagstuk maakt? Ik vermoed het laatste.
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 13:37
door tempelier
Ik zie dat ik te laat ben.
Dit kreeg ik ook nog.
x+y=2
\(x=1-\sqrt{2} \quad , \quad y=1+\sqrt{2}\)
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 13:42
door Xilvo
\(1-\frac{1}{2}\sqrt{2}\) en \(1+\frac{1}{2}\sqrt{2}\), volgens mij.
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 14:01
door ukster
Xilvo schreef: ↑zo 01 aug 2021, 13:25
Mooi! Zelf gevonden?
Nee 
De uitwerking op zichzelf is doodsimpel..
maar kom er maar eens op!
Ik kan me (nog) geen voorstelling maken bij zo'n complex snijpunt.
Misschien vinden we hierin het antwoord
Re: vergelijkingen
Geplaatst: zo 01 aug 2021, 14:02
door tempelier
Xilvo schreef: ↑zo 01 aug 2021, 13:42
\(1-\frac{1}{2}\sqrt{2}\) en
\(1+\frac{1}{2}\sqrt{2}\), volgens mij.
Stomme typefout sorry.