1 van 7
weerstanden
Geplaatst: zo 15 aug 2021, 16:27
door ukster
Elk van de vier netwerken gebruikt dezelfde vier verschillende weerstanden a,b,c,d∈N
De vervangingsweerstand van de netwerken zelf zijn respectievelijk ook weer a,b,c,d
Welke waarde(n) van a,b,c,d voldoet hieraan?
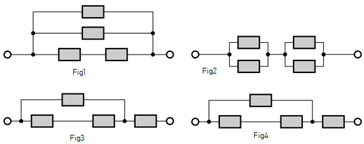
- weerstandsnetwerk 4147 keer bekeken
Dit lijkt me typisch een (uitputtende)computerklus of ligt een oplossing toch voor de hand?
Re: weerstanden
Geplaatst: zo 15 aug 2021, 17:31
door Xilvo
Lijkt me een omvangrijke klus.
Weerstand 0 mag ook? De laatste twee schakelingen zijn met opzet gelijk maar moeten andere waardes opleveren?
Re: weerstanden
Geplaatst: zo 15 aug 2021, 20:08
door WillemB
Wellicht valt het nog mee, je hebt per schakeling 16 mogelijkheden, totaal 64,
daar zitten dubbelIngen in, zo te zien houd je dan totaal van de 4 schakeling 4 mogelijkheden per schakeling over.
Je kan dat in een spreadsheet zetten, met de 4x4 is 16 uitkomsten,
dan kan je met de vier variabelen a,b,c,d spelen tot uit de 16 mogelijke uitkomsten,
weer 4 keer a, b,c en d uitkomt.
Op goed geluk 1, 2, 3 en 4 ohm, krijg je al 1 ongeveer 2 ongeveer 3 en ongeveer 4.
Re: weerstanden
Geplaatst: zo 15 aug 2021, 20:21
door Xilvo
Voor de eerste schakeling zijn er 6 mogelijkheden, voor de tweede 3 en voor de laatste twee ieder 12 mogelijkheden.
Dat voor allerlei mogelijkheden voor a, b, c en d.
Ik heb de computer aan het werk gezet en denk/programmeerfouten voorbehouden, heb ik nog geen oplossingen gevonden waarbij alle weerstanden groter dan 0 zijn. Met een weerstand van nul erbij zijn er veel oplossingen.
Re: weerstanden
Geplaatst: zo 15 aug 2021, 22:21
door ukster
WillemB schreef: ↑zo 15 aug 2021, 20:08
Wellicht valt het nog mee, je hebt per schakeling 16 mogelijkheden, totaal 64,
daar zitten dubbelingen in, zo te zien houd je dan totaal van de 4 schakeling 4 mogelijkheden per schakeling over.
Je kan dat in een spreadsheet zetten, met de 4x4 is 16 uitkomsten,
dan kan je met de vier variabelen a,b,c,d spelen tot uit de 16 mogelijke uitkomsten,
weer 4 keer a, b,c en d uitkomt.
Op goed geluk 1, 2, 3 en 4 ohm, krijg je al 1 ongeveer 2 ongeveer 3 en ongeveer 4.
Met jouw 'op goed geluk' waardes lukt het inderdaad.
Ik weet niet of dat de enige oplossing is
Re: weerstanden
Geplaatst: ma 16 aug 2021, 11:25
door Xilvo
Helaas, het programma bevatte een foutje. Het had de oplossing 1,2,3,4 natuurlijk meteen moeten vinden.
Alle veelvouden van 1, 2, 3, 4 zoals 4, 8, 12, 16 zijn natuurlijk ook oplossingen.
Verder zijn er oplossingen met een weerstand van nul Ohm, zoals 0, 2, 3, 6 en alle veelvouden daarvan.
Hier de oplossingen die ik vond met weerstanden tot 40 Ohm:
4 3 2 1
6 3 2 0
8 6 4 2
12 4 3 0
12 6 4 0
12 9 6 3
15 10 6 0
16 12 8 4
18 9 6 0
20 5 4 0
20 15 10 5
24 8 6 0
24 12 8 0
24 18 12 6
28 21 12 0
28 21 14 7
30 6 5 0
30 15 10 0
30 20 12 0
32 24 16 8
35 14 10 0
36 12 9 0
36 18 12 0
36 27 18 9
Re: weerstanden
Geplaatst: ma 16 aug 2021, 12:01
door WillemB
Er zal wel enige logica inzitten, daar de schakelingen niet zo willekeurig lijken.
Tenslotte moeten de weerstanden een oplopende waarde hebben, dus stel: a<b<c<d
wat schakeling 1 al tot de laagste waarde laat zijn, vrijwel alles parallel.
Dus schakeling 1 heeft de waarde a.
De tweede met twee parallel in serie, komt dan op de tweede plaats met b.
De derde en vierde, omdat er altijd 1 weerstand in serie staat op c en d.
Dan nog zoeken naar andere verbanden..?
Re: weerstanden
Geplaatst: ma 16 aug 2021, 16:12
door Professor Puntje
ukster schreef: ↑zo 15 aug 2021, 16:27
Elk van de vier netwerken gebruikt dezelfde vier verschillende weerstanden a,b,c,d∈N
De vervangingsweerstand van de netwerken zelf zijn respectievelijk ook weer a,b,c,d
Dit betekent dat je bij elk van deze netwerken één van de weerstanden door het netwerk zelf kunt vervangen, en dat je dat zelfs tot in het oneindige kunt blijven herhalen zonder dat de vervangweerstand van dat steeds omvangrijker wordende netwerk verandert...
Re: weerstanden
Geplaatst: ma 16 aug 2021, 16:23
door ukster
Dat moet dan wel de weerstand zijn met dezelfde waarde als de vervangingsweerstand van het netwerk
Re: weerstanden
Geplaatst: ma 16 aug 2021, 16:30
door Professor Puntje
Inderdaad. Maar zo kun je door te kijken of de vervangweerstand van het netwerk door een substitutie verandert wel veel schijnbare mogelijkheden schrappen.
Re: weerstanden
Geplaatst: do 19 aug 2021, 21:27
door Professor Puntje
Heeft er iemand al een slimme oplossingswijze gevonden? Ik zelf nog niet, maar het vraagstuk fascineert me wel...
Re: weerstanden
Geplaatst: do 19 aug 2021, 21:33
door Xilvo
Ik niet. Numeriek blijken alle oplossingen tot die met een maximale weerstand van 700 Ohm en alle weerstanden groter dan 0 Ohm, veelvouden van 1, 2, 3 en 4 Ohm te zijn.
Maar dan heb je er nog oneindig veel te doen.
Re: weerstanden
Geplaatst: do 19 aug 2021, 21:49
door Professor Puntje
OK - dan ga ik er van het weekend eens verder naar kijken. Normaal gesproken is het de bedoeling zoiets met een of ander slimmigheidje op te lossen. Tenzij ukster dit vraagstuk zelf in elkaar heeft gezet om ons te foppen....
Re: weerstanden
Geplaatst: do 19 aug 2021, 22:01
door Professor Puntje
Moeten de oplossingen eigenlijk wel vier verschillende gehele getallen groter dan nul zijn?
Re: weerstanden
Geplaatst: do 19 aug 2021, 22:06
door Xilvo
Professor Puntje schreef: ↑do 19 aug 2021, 22:01
Moeten de oplossingen eigenlijk wel vier verschillende
gehele getallen groter dan nul zijn?
"vier verschillende weerstanden a,b,c,d ∈ N"
Nul mag, verschillend moet. Ook voor de vier schakelingen, anders was de laatste overbodig.