1 van 5
dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 10:55
door jorian5000
Hey hallo,
Ik ben bezig met een project en loop een beetje vast in de sterkteleer.

De situatie is als volgt:

A en D zijn een inklemming.
F is 8090N
AB = 624 mm
BC =2974 mm
CD = 624 mm
L = 4222mm
Volledig symmetrisch dus.
Wat ik wil bepalen is de doorbuiging op punt B en C. ik kan me heugen dat ik ooit heb geleerd hoe je een doorbuiging uitrekent op elk punt in een balk maar ik ben het goed kwijt.
Elke vorm van hulp wordt gewaardeerd.
Groet, Jorian
Re: dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 12:30
door Rola
Afbeelding ontbreekt.
Re: dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 12:56
door jorian5000
Bij deze nogmaals het figuur
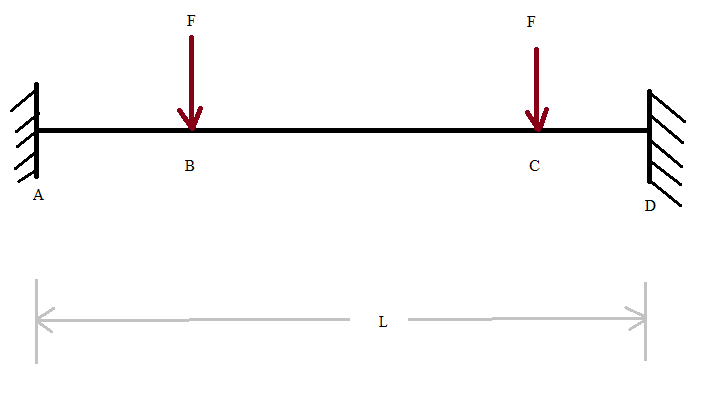
- Naamloos 7717 keer bekeken
Re: dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 14:26
door Gast
Materiaaleigenschappen ontbreken.
Re: dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 14:32
door Gast
Dan zou je wat met de
vergeet me nietjes kunnen spelen. Een kant losmaken geloof ik, uhm .. hoe precies ben ik dus
wel vergeten bij volledige fixatie aan beide kanten.
Zie reactie hier (niet doorgenomen, maar ik neem gemakshalve aan dat het klopt):
viewtopic.php?t=173051
Of gebruik dit .. waar je verder weinig van leert:
https://amesweb.info/Beam/fixed-beam-de ... lator.aspx
Re: dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 15:43
door jorian5000
Gast044 schreef: ↑di 12 okt 2021, 14:32
Dan zou je wat met de
vergeet me nietjes kunnen spelen. Een kant losmaken geloof ik, uhm .. hoe precies ben ik dus
wel vergeten bij volledige fixatie aan beide kanten.
Zie reactie hier (niet doorgenomen, maar ik neem gemakshalve aan dat het klopt):
viewtopic.php?t=173051
Of gebruik dit .. waar je verder weinig van leert:
https://amesweb.info/Beam/fixed-beam-de ... lator.aspx
Ja precies, dat een kant losmaken ontgaat mij ook volledig. weet ook niet meer hoe het heet als je dat doen.
ik ben dat topic ook tegen gekomen maar daar werd ik niet wijzer uit. misschien interpreteer ik het verkeerd maar het lijkt mij vooral te gaan over de momentlijn en niet over de specifieke verplaatsing op een punt.
Re: dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 15:49
door jorian5000
Voor de volledigheid toch nog even wat verdere eigenschappen.
het profiel is een CHS 88.9x5. een buis met buiten maat 88,9mm en een 5mm wanddikte de "i" wordt dan 6,337*10^5 mm^4
E gaan ik uit van 200GPa
Re: dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 18:12
door Gast
Ik zal het zelf nooit te nimmer weer gebruiken, want ja .. computer.
(Daarom vergeet "iedereen" die
vergeet me nietjes tegenwoordig ook bijna allemaal).
Maar volgens mij is dit correct:
https://mathalino.com/reviewer/strength ... rated-load
En moet het daarmee lukken.
Re: dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 20:50
door wnvl1
Maar als je teruggrijpt naar de basisformules, lijkt het mij mee te vallen om die formules jaren later nog te kunnen reconstrueren.
$$\frac{d^{2} y}{d x^{2}}=\frac{M}{EI}$$
Hier hebben we
$$M = F \mid AB \mid - x F$$
op het eerste stuk van de balk.
Nu twee keer integreren en randvoorwaarde
$$\frac{dy}{d x} (0)=0$$
Re: dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 21:45
door Gast
Huh?
Maar het gaat om de afbuiging, waarbij ik nog steeds niet precies weet hoe dat op punt B en C zit trouwens .. alleen exact in het midden.
Re: dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 21:55
door wnvl1
Als je dat integreert heb je toch de volledige lijn van de balk en dan heb je toch op elk punt de afbuiging. Doe maar eens...
Re: dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 23:05
door Gast
Lukt me niet, geef het op. Kun je t even voordoen?
Als dat klopt zou wel mooi zijn, maar begrijp ik niet waarom "niemand" dat ooit zo geleerd wordt.
Re: dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 23:24
door wnvl1
$$\frac{d^{2} y}{d x^{2}}=\frac{M}{EI}$$
$$\frac{d^{2} y}{d x^{2}}=\frac{F \mid AB \mid - x F}{EI}$$
Twee keer integreren
$$y=\frac{F }{EI} \left(\frac{\mid AB \mid x^2}{2} - \frac{x^3}{6} + C_1x + C_2 \right) $$
Randvoorwaarden zijn \(\frac{dy}{d x} (0)=0\) en \(y(0) = 0\).
Dus
$$y=\frac{F }{EI} \left(\frac{\mid AB \mid x^2}{2} - \frac{x^3}{6} \right)$$
Je vult nu bvb \(x= \mid AB \mid\) in, en je krijgt nu terhoogte van \(\mid AB \mid\) de uitwijking. Je komt daar dan op \(\frac{F }{EI} \left(\frac{\mid AB \mid ^3}{3} \right)\)
Voorbij \(\mid AB \mid\) is het moment 0, dus ik denk dat je nu de methode gemakkelijk kan uitbreiden om de uitwijking in het midden te berekenen. Je stelt continuiteitsvoorwaarden op voor de eerste afgeleide ter hoogte van \(\mid AB \mid \)...
Re: dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 23:28
door wnvl1
Gast044 schreef: ↑di 12 okt 2021, 23:05
Als dat klopt zou wel mooi zijn, maar begrijp ik niet waarom "niemand" dat ooit zo geleerd wordt.
Dit staat echt wel zo in een cursus sterkteleer op ingenieursniveau. Ik snap wel dat je op het niveau van het secundair onderwijs eerder met tabelletjes gaat werken.
Re: dubbele inklemming en 2 belastingen
Geplaatst: di 12 okt 2021, 23:40
door Gast
Ik weet niet welke opleiding jij genoten hebt. Dat zal dan een master zijn, want een Bachelor (WTB) heb ik gedaan en ik garandeer je dat dat nooit ergens zo gestaan heeft of uitgelegd is. (Ik heb de boeken geloof ik nog ergens.)
Maar ik ben doodmoe, zal het later doornemen.


