1 van 12
Projectielbaan
Geplaatst: vr 22 okt 2021, 19:03
door ukster
Het is windstil.
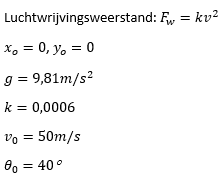
- Projectielbaan1 8729 keer bekeken
Er is sprake van niet lineaire gekoppelde bewegingsvergelijkingen. Derhalve kent de projectielbaan geen exacte analytische oplossing en moet dus numeriek worden opgelost.
Wel heb ik een analytische benadering toegepast en daarmee berekend:

- Projectielbaan2 8729 keer bekeken
Ik wil weten of de resultaten minder dan 3% afwijken van de numeriek verkregen waarde.
Iemand op dit Forum die dit numeriek kan/wil bevestigen?
Re: Projectielbaan
Geplaatst: vr 22 okt 2021, 19:17
door Xilvo
Wat is de massa?
Re: Projectielbaan
Geplaatst: vr 22 okt 2021, 19:25
door wnvl1
Je hebt dus
$$
m\ddot{x} = -0.0006 \dot{x}^2 \\
m\ddot{y} = -0.0006 \dot{y}^2 - g
$$
Beginvoorwaarden:
$$
\dot{x}(0) = 50 \cos(40) \\
x(0) = 0 \\
\dot{y}(0) = 50 \sin(40) \\
y(0) = 0 \\
$$
dat opgelost moet worden.
Re: Projectielbaan
Geplaatst: vr 22 okt 2021, 20:08
door ukster
Foutje inderdaad...
Deze definitie voor k is gebruikt in de toegepaste formules.
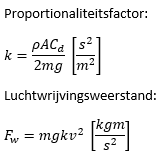
- proportionaliteitsfactor 8689 keer bekeken
Re: Projectielbaan
Geplaatst: vr 22 okt 2021, 20:10
door Xilvo
wnvl1 schreef: ↑vr 22 okt 2021, 19:25
Je hebt dus
$$
m\ddot{x} = -0.0006 \dot{x}^2 \\
m\ddot{y} = -0.0006 \dot{y}^2 - g
$$
Dat lijkt me niet goed. Dan is de richting van de kracht
\(\arctan{\frac{y^2}{x^2}}\) en niet parallel aan de bewegingsrichting.
Re: Projectielbaan
Geplaatst: vr 22 okt 2021, 20:12
door wnvl1
Inderdaad is niet goed.
Re: Projectielbaan
Geplaatst: vr 22 okt 2021, 20:26
door wnvl1
$$m\ddot{x} = -0.0006 \dot{x} \sqrt{\dot{x}^2 + \dot{y}^2} \\
m\ddot{y} = -0.0006 \dot{y}\sqrt{\dot{x}^2 + \dot{y}^2} - g$$
Re: Projectielbaan
Geplaatst: vr 22 okt 2021, 20:33
door wnvl1
Ik kom op zoiets in Matlab.
f = @(t,y) [y(2); -9.81*0.0006*y(2)*(y(2)^2+y(4)^2);y(4);-9.81*0.0006*y(4)*(y(2)^2+y(4)^2) - 9.81 ];
tspan = [0, 10];
yinit = [0, 50*cosd(40), 0, 50*sind(40)];
[t,y]=ode45(f, tspan, xinit)
plot(y(:,1),y(:,3))
Re: Projectielbaan
Geplaatst: vr 22 okt 2021, 20:37
door Xilvo
Ik krijg zoiets met Python.
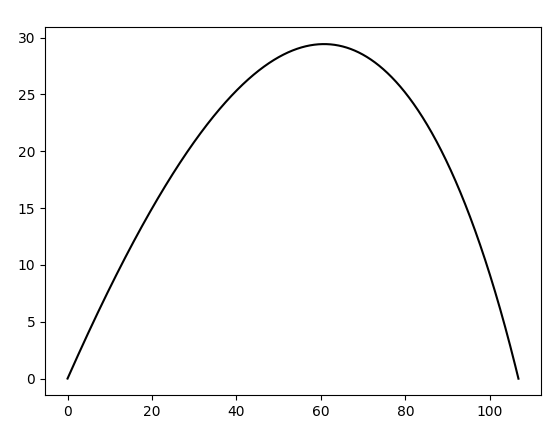
- projectielbaan 8658 keer bekeken
Dan is L=106,75 m, dat komt dus niet overeen met wat Ukster vindt.
En de maximale hoogte is anders dan wat wnvl1 vindt.
Re: Projectielbaan
Geplaatst: vr 22 okt 2021, 20:38
door wnvl1
Wil je de code evt delen dan kijk ik eens naar het verschil met Matlab?
Re: Projectielbaan
Geplaatst: vr 22 okt 2021, 20:44
door Xilvo
Dit is de essentie.
'kk' is de k van Ukster, ik had al wat geschreven en heb dat aangepast aan de informatie die later kwam.
m is 1, maar dat moet niet uitmaken.
Code: Selecteer alles
def run(m):
dt=0.001
t=0
x=0
y=0
g=9.81
k=0.0006
kk=m*g*k
v0=50
th=40
thr=np.deg2rad(th)
vx=v0*np.cos(thr)
vy=v0*np.sin(thr)
tr=[0]
xr=[0]
yr=[0]
while y>=0:
v2=vx**2+vy**2
Fw=kk*v2
Fx=-Fw*vx/np.sqrt(v2)
Fy=-Fw*vx/np.sqrt(v2)-g*m
vx+=dt*Fx/m
vy+=dt*Fy/m
x+=dt*vx
y+=dt*vy
t+=dt
xr.append(x)
yr.append(y)
tr.append(t)
return tr, xr,yr
Re: Projectielbaan
Geplaatst: vr 22 okt 2021, 22:40
door wnvl1
Het moet zijn
Fy=-Fw*vy/np.sqrt(v2)-g*m
ipv vx
Re: Projectielbaan
Geplaatst: za 23 okt 2021, 00:00
door wnvl1
Ik zag dat je in python ook een solver hebt voor systemen van differentiaalvergelijkingen
Code: Selecteer alles
from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt
def vectorfield(w, t):
x, dxdt, y, dydt = w
# Create f = (x1',y1',x2',y2'):
f = [dxdt,
-9.81 * 0.0006 * dxdt * (dxdt ** 2 + dydt ** 2),
dydt,
-9.81 * 0.0006 * dydt * (dxdt ** 2 + dydt ** 2) - 9.81]
return f
# Initial conditions
# x1 and x2 are the initial displacements; y1 and y2 are the initial velocities
x = 0
dxdt = 50*np.cos(np.deg2rad(40))
y = 0
dydt = 50*np.sin(np.deg2rad(40))
# ODE solver parameters
abserr = 1.0e-8
relerr = 1.0e-6
stoptime = 10.0
numpoints = 250
# Create the time samples for the output of the ODE solver.
# I use a large number of points, only because I want to make
# a plot of the solution that looks nice.
t = [stoptime * float(i) / (numpoints - 1) for i in range(numpoints)]
# Pack up the parameters and initial conditions:
w0 = [x, dxdt, y, dydt]
# Call the ODE solver.
wsol = odeint(vectorfield, w0, t,
atol=abserr, rtol=relerr)
print(wsol)
x = [row[0] for row in wsol]
y = [row[2] for row in wsol]
plt.plot(x,y)
plt.show()
Dan krijg ik deze oplossing.
Er is precies een klein verschilletje tussen de python en de matlab oplossing.
Re: Projectielbaan
Geplaatst: za 23 okt 2021, 00:22
door wnvl1
Ik was in beiden nog een wortel vergeten.
Matlab
Python
Code: Selecteer alles
f = @(t,y) [y(2); -9.81*0.0006*y(2)*(y(2)^2+y(4)^2)^0.5;y(4);-9.81*0.0006*y(4)*(y(2)^2+y(4)^2)^0.5 - 9.81 ];
tspan = [0, 15];
yinit = [0, 50*cosd(40), 0, 50*sind(40)];
[t,y]=ode45(f, tspan, xinit)
plot(y(:,1),y(:,3))
Code: Selecteer alles
from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt
def vectorfield(w, t):
x, dxdt, y, dydt = w
f = [dxdt,
-9.81 * 0.0006 * dxdt * (dxdt ** 2 + dydt ** 2)**0.5,
dydt,
-9.81 * 0.0006 * dydt * (dxdt ** 2 + dydt ** 2)**0.5 - 9.81]
return f
# Initial conditions
x = 0
dxdt = 50*np.cos(np.deg2rad(40))
y = 0
dydt = 50*np.sin(np.deg2rad(40))
# ODE solver parameters
abserr = 1.0e-8
relerr = 1.0e-6
stoptime = 15.0
numpoints = 250
# Create the time samples for the output of the ODE solver.
# I use a large number of points, only because I want to make
# a plot of the solution that looks nice.
t = [stoptime * float(i) / (numpoints - 1) for i in range(numpoints)]
# Pack up the parameters and initial conditions:
w0 = [x, dxdt, y, dydt]
# Call the ODE solver.
wsol = odeint(vectorfield, w0, t,
atol=abserr, rtol=relerr)
print(wsol)
x = [row[0] for row in wsol]
y = [row[2] for row in wsol]
plt.plot(x,y)
plt.show()
Re: Projectielbaan
Geplaatst: za 23 okt 2021, 09:48
door Xilvo
wnvl1 schreef: ↑vr 22 okt 2021, 22:40
Het moet zijn
Fy=-Fw*
vy/np.sqrt(v2)-g*m
ipv vx
Klopt!