1 van 1
bewijs
Geplaatst: di 16 nov 2021, 17:07
door ukster
bewijs:
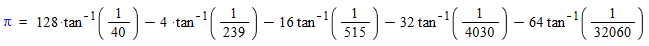
- Bewijs 1679 keer bekeken
Kan het bewijs alleen geleverd worden via de integraalvorm ?
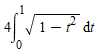
- integraalvorm 1679 keer bekeken
Re: bewijs
Geplaatst: di 16 nov 2021, 18:13
door tempelier
Nee.
Wat bedoel je met -1? de inverse 0f de reciproke (wat correctt zou zijn)
Probeer dit eens.
De afgeleide moet 0 zijn.
Re: bewijs
Geplaatst: di 16 nov 2021, 18:23
door ukster
tempelier schreef: ↑di 16 nov 2021, 18:13
Wat bedoel je met -1? de inverse 0f de reciproke (wat correctt zou zijn)
de inverse functie (dus arctan)
Re: bewijs
Geplaatst: di 16 nov 2021, 18:35
door tempelier
Puntje en ik vinden dat een incorrecte notatie, maar dat is een andere discussie.
Blijft zo dat als je differentieert het rechter lid nul moet zijn.
Hierdoor wordt de vergelijking algebraïsch.
Re: bewijs
Geplaatst: di 16 nov 2021, 18:39
door Xilvo
tempelier schreef: ↑di 16 nov 2021, 18:35
Blijft zo dat als je differentieert het rechter lid nul moet zijn.
Wat wil je waarnaar differentiëren? Ik zie geen variabele.
Re: bewijs
Geplaatst: di 16 nov 2021, 19:15
door wnvl1
Links en rechts tangens nemen.
En dan heel dikwijls toepassen van
$$\tan (x+y) = \frac{\tan(x)+tan(y)}{1-\tan(x)\tan(y)} $$
$$\tan (2x) = \frac{2\tan(x)}{1-\tan^2(x)} $$
$$\tan (\arctan(x))=x$$
Zo ga je dat altijd wel kunnen bewijzen.
Dat is nu wel niet echt een mooi bewijs.
Re: bewijs
Geplaatst: di 16 nov 2021, 19:25
door wnvl1
Hoe werkt trouwens het bewijs via die integraalvorm?
Re: bewijs
Geplaatst: di 16 nov 2021, 20:02
door ukster
ik vond deze gelijkheid.
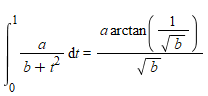
- gelijkheid 1550 keer bekeken
En dan de 5 componenten van de te bewijzen uitdrukking onderbrengen in 1 integraal van 0 tot 1 met π als resultaat.
Maar is dat een geldig bewijs?
Re: bewijs
Geplaatst: di 16 nov 2021, 21:07
door wnvl1
Dan krijg je een bepaalde integraal met 5 breuken, en dan?
Re: bewijs
Geplaatst: di 16 nov 2021, 21:12
door ukster
met π als resultaat
Re: bewijs
Geplaatst: di 16 nov 2021, 21:38
door RedCat
Alternatief:
Herschrijf de vergelijking:
\(\small \frac{\pi}{4} = 32 \tan^{-1}\left( \frac{1}{40} \right) - \tan^{-1}\left( \frac{1}{239} \right) - 4\tan^{-1}\left( \frac{1}{515} \right)-8\tan^{-1}\left( \frac{1}{4030} \right)-16\tan^{-1}\left( \frac{1}{32060} \right)\)
Pas rechts op elke term herhaald de verdubbelingsformule toe
(resp. 5, 0, 2, 3 en 4 keer op elk van de termen):
\(\small 2\tan^{-1}\left( \frac{a}{b} \right) = \tan^{-1}\left( \frac{2ab}{b^2-a^2} \right) \)
Trek tenslotte rechts alle termen samen met
\(\small \tan^{-1}\left( \frac{a}{b} \right) + \tan^{-1}\left( \frac{c}{d} \right) = \tan^{-1}\left( \frac{ad+bc}{bd-ac} \right) \)
Dat levert:
\(\small \frac{\pi}{4} = \tan^{-1}\left( 1 \right)\)
Re: bewijs
Geplaatst: di 16 nov 2021, 21:53
door ukster
wnvl1 schreef: ↑di 16 nov 2021, 21:07
Dan krijg je een bepaalde integraal met 5 breuken, en dan?
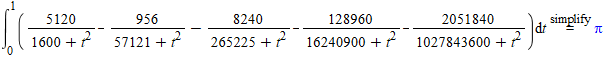
- pi 1461 keer bekeken
Re: bewijs
Geplaatst: di 16 nov 2021, 22:24
door wnvl1
@ukster Maar dan is de vraag hoe reken die integraal uit zonder terug te passeren via de arctangensen uit de initiele oefening? Nu lost je reken pakket het probleem op voor jou.
Misschien biedt complexe analyse hiervoor wel een uitweg...
https://nl.wikipedia.org/wiki/Residu_(functietheorie)