1 van 2
bank
Geplaatst: di 27 feb 2024, 16:02
door ukster
Wat is de maximale lengte van een rechthoekige zitbank van 1m breed welke horizontaal verplaatst wordt (zonder vervorming) door een L-vormige gang met breedte 1,82m en 1,21m
Volgens wolfram mathematica is het 2,2021m
Mijn analytische oplossing geeft 2,2373m. best wel een significant verschil vind ik.
Re: bank
Geplaatst: di 27 feb 2024, 16:50
door Xilvo
Numeriek kom ik op 2,20205
Re: bank
Geplaatst: di 27 feb 2024, 18:06
door ukster
Dan moet hierin dus ergens een fout zitten!
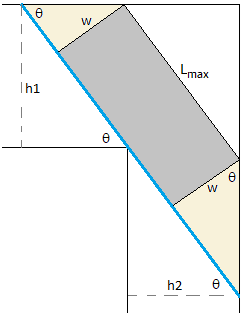
- bank 1478 keer bekeken
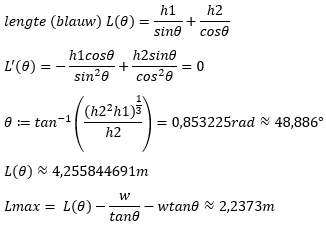
- bank1 1478 keer bekeken
Re: bank
Geplaatst: di 27 feb 2024, 18:10
door Xilvo
Ik heb er nog niet uitgebreid naar gekeken maar betekent \(L'(\theta)=0\) ook dat \(L\) minimaal is?
Anders gezegd, is een extreem van de blauwe lijn ook een extreem voor \(L\) ?
Re: bank
Geplaatst: di 27 feb 2024, 18:17
door ukster
volgens mij levert het de hoek op waarbij L(θ) minimaal is
Re: bank
Geplaatst: di 27 feb 2024, 18:28
door Xilvo
ukster schreef: ↑di 27 feb 2024, 18:17
volgens mij levert het de hoek op waarbij L(θ) minimaal is
Waarschijnlijk klopt dat als de twee gangdelen even breed zijn.
Deze moet een extreme waarde (minimum) hebben:
\(L=\frac{h_1}{\sin \theta}+\frac{h_2}{\cos \theta}-\frac{1}{\cot \theta}-\frac{1}{\tan \theta}\)
Re: bank
Geplaatst: di 27 feb 2024, 18:40
door ukster
Xilvo schreef: ↑di 27 feb 2024, 18:28
\(L=\frac{h_1}{\sin \theta}+\frac{h_2}{\cos \theta}-\frac{1}{\cot \theta}-\frac{1}{\tan \theta}\)
en dat is 2,2373 m
Re: bank
Geplaatst: di 27 feb 2024, 18:48
door Xilvo
Ook voor deze formule vind ik numeriek weer een minimale lengte van 2,20205 m
Re: bank
Geplaatst: di 27 feb 2024, 18:57
door ukster
met h1=1,82m h2=1,21m en θ=48.886° is de uitkomst toch echt 2,2373m
Re: bank
Geplaatst: di 27 feb 2024, 19:02
door Xilvo
Bij die hoek vind ik inderdaad ook 2,2373 m.
Maar bij een hoek van 56,204° kom ik op de (kortere) 2,20205 m.
Re: bank
Geplaatst: di 27 feb 2024, 19:14
door ukster
Xilvo schreef: ↑di 27 feb 2024, 19:02
Maar bij een hoek van 56,204° kom ik op de (kortere) 2,20205 m.
56,204° ??
Re: bank
Geplaatst: di 27 feb 2024, 19:18
door Xilvo
Als ik het numeriek nog iets nauwkeuriger doe kom ik op 56,2038°. Maar goed, dat ligt zo dicht bij elkaar...
Re: bank
Geplaatst: di 27 feb 2024, 19:20
door ukster
dat is dan de hoek die ik in mijn uitwerking mis.
Hoe kom je aan die hoek?
Re: bank
Geplaatst: di 27 feb 2024, 19:24
door Xilvo
ukster schreef: ↑di 27 feb 2024, 19:20
dat is dan de hoek die ik in mijn uitwerking mis.
Hoe kom je aan die hoek?
Door heel primitief met kleine stapjes het hoekbereik van 5 tot 85° voor
\(\theta\) te doorlopen voor
\(L=\frac{h_1}{\sin \theta}+\frac{h_2}{\cos \theta}-\frac{1}{\cot \theta}-\frac{1}{\tan \theta}\)
en te onthouden waar
\(L\) de laagste waarde heeft.
Re: bank
Geplaatst: di 27 feb 2024, 19:33
door ukster
juist, dus 48,886°is niet de hoek waarbij de blauwe lijnlengte minimaal is