1 van 2
Arbeid
Geplaatst: wo 28 feb 2024, 14:09
door ukster
Een deeltje ondervindt een kracht F met de componenten:
Fx=28x
3+55xy
2+10z
Fy=28x
3+55xy
2
Fz=10z
Hoeveel arbeid verricht F als het deeltje zich langs een rechte lijn verplaatst vanuit de oorsprong naar het punt (x0,y0,z0)=(10,26,15)
zijn dit de juiste tijdintroducties voor verplaatsing vanuit de oorsprong langs een rechte lijn?
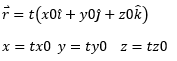
- tijdintroductie 2064 keer bekeken
Re: Arbeid
Geplaatst: wo 28 feb 2024, 18:33
door wnvl1
ja
Re: Arbeid
Geplaatst: do 29 feb 2024, 19:31
door ukster
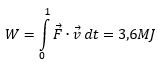
- arbeid 1915 keer bekeken
Re: Arbeid
Geplaatst: do 29 feb 2024, 22:09
door wnvl1
Een leuke uitbreiding zou zijn, wat is de minimale arbeid nodig om van (0,0,0) naar (10,26,15) te gaan?
Het traject moet dus geoptimaliseerd worden.
Re: Arbeid
Geplaatst: do 29 feb 2024, 23:03
door ukster
Interessant dat principe van minimale actie! Ik ga mij daar eens in verdiepen...om te proberen pad C te vinden
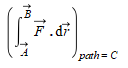
- pad C 1876 keer bekeken
Re: Arbeid
Geplaatst: do 29 feb 2024, 23:36
door wnvl1
Bij nader inzien zie ik ook nog niet direct hoe ik dat vertaald krijg naar Euler Lagrange.
Re: Arbeid
Geplaatst: vr 01 mar 2024, 00:08
door wnvl1
Ik zou het traject kunnen uitdrukken met de x-coordinaat als parameter
\(x=x\)
\(y=q_1(x)\)
\(z=q_2(x)\)
\(q_1^{\prime} = \frac{dq_1}{dx}\)
\(q_2^{\prime} = \frac{dq_2}{dx}\)
Dit is de integraal die geminimaliseerd moet worden
$$W(q_1, q_2)=\int_0^{10} F_x dx + F_ydy +F_z dz= \int_0^{10} F_x + F_y q_1^{\prime} +F_zq_2^{\prime} dx $$
$$= \int_0^{10}28x^3+55xq_1^2+10q_2 + (28x^3+55xq_1^2) q_1^{\prime} +10q_2 q_2^{\prime} dx $$
Randvoorwaarden zijn
\(q_1(0)=0\)
\(q_2(0)=0\)
\(q_1(10)=26\)
\(q_2(10)=15\)
Maar nu?
Re: Arbeid
Geplaatst: vr 01 mar 2024, 00:20
door wnvl1
Stel
$$L(x) = 28x^3+55xq_1^2+10q_2 + (28x^3+55xq_1^2) q_1^{\prime} +10q_2 q_2^{\prime}$$
Dan moet gelden volgens Euler Lagrange
$$\frac{\partial L}{\partial q_1} = \frac{\partial }{\partial x} \frac{\partial L }{\partial q_1^{\prime}} $$
en
$$\frac{\partial L}{\partial q_2} = \frac{\partial }{\partial x} \frac{\partial L }{\partial q_2^{\prime}} $$
Wordt vervolgd of gecorrigeerd...
Re: Arbeid
Geplaatst: vr 01 mar 2024, 13:40
door ukster
Heb het probleem voorgelegd aan Chatgpt met dit resultaat voor de bewegingsvergelijkingen van het vraagstuk.

- chatgpt 1778 keer bekeken
Re: Arbeid
Geplaatst: vr 01 mar 2024, 14:07
door wnvl1
Het is mooi dat chatgpt al doorheeft dat je Euler Lagrange moet gebruiken. En dat het veel werk is, daar heeft hij ook gelijk in. Voor de rest gaat hij toch nog wat les moeten volgen.
Ik reken later verder.
Re: Arbeid
Geplaatst: vr 01 mar 2024, 16:52
door wnvl1
De Euler Lagrange vergelijkingen leveren op
$$110xq_1+110xq_1^\prime = 84x^2+55q_1^2 $$
en
$$10+10q_2^\prime = 0 $$
Uit de tweede vergelijking kan ik gemakkelijk \(q_2(x)\) berekenen.
$$q_2(x) = -x + C $$
Uit de randvoorwaarde \(q_2(0)=0\) volgt \(C=0\), maar dan kan ik niet meer voldoen aan mijn voorwaaarde \(q_2(10)=15\).
Doe ik iets fout of is hier niet voldaan aan de Euler Lagrange voorwaarden? Ik denk dat het laatste sowieso het geval is, maar waar loopt het dan precies mis?
PS Opvallend is dat chatgpt die 84 en 55 uit de eerste vergelijking ook heeft.
Re: Arbeid
Geplaatst: vr 01 mar 2024, 17:14
door wnvl1
Als je logisch nadenkt, is het natuurlijk optimaal om z naar min oneindig te laten gaan dan de verplaatsing over x en y doen en dan z terug naar 15 laten gaan. De optimale oplossing is niet differentieerbaar, dus er is niet voldaan aan Euler Lagrange. De opgave zou aangepast moeten worden naar een andere definitie van de kracht om er een beter raadsel van te maken.
Re: Arbeid
Geplaatst: vr 01 mar 2024, 19:03
door Xilvo
Het is geen conservatief veld. Dan kun je zoveel energie winnen of verliezen als je maar wil.
Re: Arbeid
Geplaatst: vr 01 mar 2024, 19:22
door wnvl1
Dat klopt in de zin dat je rondjes kan blijven maken om oneindig veel energie te winnen of te verliezen.
Met mijn parametrisatie
\(x=x\)
\(y=q_1(x)\)
\(z=q_2(x)\)
is er wel ruimte om tot oplossingen te komen waarbij de x-waarde niet achteruitgaat. Dan moet het wel mogelijk zijn om een leuke opgave te bedenken die tot een niet oneindige oplossing leidt, denk ik.
Re: Arbeid
Geplaatst: vr 01 mar 2024, 20:12
door wnvl1
Probleem is dat ik maar 2 integratieconstanten krijg, maar wel met 4 randvoorwaarden zit.
Dat lukt alleen maar met een oefening die 'toevallig' gemaakt is dat 2 randvoorwaaarden automatisch voldaan zijn.
Ofwel moet je de oefening dusdanig formuleren dat je de y en z coordinaat op de plek van aankomst vrijlaat.