1 van 3
Oneindige som
Geplaatst: zo 07 jul 2024, 18:09
door aljechin
Hallo iedereen
op het net kwam ik het volgende "redenering" tegen:
S = 1 + 2 + 4 + 8 +...
Bereken S.
Als "oplossing" werd gegeven:
S = 1 + 2 ( 1 + 2 +4 + ...) = 1 + 2 S
S = -1 ?
Waar zit de fout in deze redenering/methode?
Dank voor een reactie.
Re: Oneindige som
Geplaatst: zo 07 jul 2024, 18:53
door ukster
Omdat de reden r>1 divergeert de reeks, d.w.z. de som S gaat naar oneindig.
Het is dan niet correct om algebraïsche bewerkingen toe te passen zoals je zou doen met een convergente som.
Re: Oneindige som
Geplaatst: zo 07 jul 2024, 19:05
door aljechin
Beste
Dank voor uw snel en helder antwoord.
Vriendelijke groeten
Aljechin
Re: Oneindige som
Geplaatst: ma 15 jul 2024, 13:52
door jwilbers
Ik zie waar t vanaf komt, maar het is heel specifiek.
Het komt uit een binair stelsel, maar verkeerd gebruikt.
Als je +1+2+4+8+16+32+64+128 optelt en dit in een signed byte stopt dan krijg je idd -1.
Maar t rammelt aan alle kanten.
Logischerwijs gaat deze reeeks idd naar oneindig.
groeten
jeroen
Re: Oneindige som
Geplaatst: ma 15 jul 2024, 15:18
door Bart23
Een oneindige som is zinvol als de rij van partieelsommen convergeert naar een getal. In dit voorbeeld is de rij van partieelsommen: 1, 1+2, 1+2+4, 1+2+4+8,..., dus 1, 3, 7, 15,...
Convergeren naar een getal wil zeggen dat de afstand tot dat getal willekeurig klein kan worden. Het woordje 'afstand' is hier van belang. Wat bedoel je met afstand? Normaal gebruiken we als afstand tussen 2 getallen a en b de absolute waarde van a-b. Dus de afstand tussen 3 en 15 is |3-15|=12. Deze (meestal gebruikte) afstand is de zogenaamde euclidische afstand. Maar je kan ook andere soorten afstand gebruiken.
Bijvoorbeeld de 2-adische afstand bij rationale getallen a en b. In plaats van de absolute waarde te nemen kijken we naar de hoogste macht van 2 die in de teller van a-b voorkomt, noem deze even m. De 2-adische afstand tussen a en b wordt dan gedefinieerd als 1/2m. Om met dezelfde getallen te werken: de 2-adische afstand tussen 3 en 15 vinden door 3-15=-12 zoveel mogelijk te delen door 2. 4 kan maar 8 niet meer, de afstand is dus 1/8.
Zo vinden we de afstand tussen:
-1 en 1 ---> 1- (-1)=2 dus afstand is 1/2
-1 en (1+2) ---> (1+2)-(-1)=4 dus afstand is 1/4
-1 en (1+2+4) --->(1+2+4)-(-1)=8 dus afstand is 1/8
Zo zie je dat 1+2+4+8+.. zo dicht als je maar wil bij -1 ligt (in 2-adische afstand) en dat je dus wel degelijk kunt zeggen dat -1=1+2+4+8+...
In de juiste context natuurlijk.
Iets gelijkaardig, maar niet hetzelfde, heb je bij bv de som van Ramanujan 1+2+3+4+5+6+...=-1/12
Re: Oneindige som
Geplaatst: ma 15 jul 2024, 16:03
door Bart23
Vervelend dat je je eigen berichten na korte tijd niet meer kan aanpassen. Een nieuwe post dan maar.
De 2-adische afstand tussen 3 en 15 vinden door 3-15=-12 zoveel mogelijk te delen door 2. 4 kan maar 8 niet meer, de afstand is dus 1/4
Re: Oneindige som
Geplaatst: ma 15 jul 2024, 16:20
door Xilvo
Waarom zou je zo'n 2-adische afstand gebruiken?
Kun je op dezelfde manier niet beredeneren dat de 2-adische afstand van 1+2+4+... met -2 tot nul nadert?
Re: Oneindige som
Geplaatst: ma 15 jul 2024, 16:58
door Bart23
Nee, in een metrische ruimte kan een rij hoogstens één limiet hebben. In dit voorbeeld:
-2 en 1 ---> 1- (-2)=3 dus afstand is 1/2^0=1
-2 en (1+2) ---> (1+2)-(-2)=5 dus afstand is 1/2^0=1
-2 en (1+2+4) --->(1+2+4)-(-2)=7 dus afstand is 1/2^0=1
algemeen 1+2+...+2^n - (-2)=2^(n+1)+1 heeft nooit een factor 2, dus elke partiële som heeft afstand 1 tot -2 (of tot eender welk even getal)
Deze afstand/norm heeft veel nut in getaltheorie. Het laat toe om binnen getaltheorie te werken met reeksen en zo een vorm van analyse binnen te brengen, de zgn p-adische analyse. Met veel analogieën tussen de gewone en die nieuwe analyse. Bv het lemma van Hensel om nulpunten te vinden van veeltermen modulo p is analoog aan de nulpunten benaderingsmethode van Newton. Ook een interessant verband is het local-global principle van Hasse dat voor sommige soorten vergelijking zegt dat er een oplossing in de rationale getallen bestaat als en slechts als er een oplossing is in de reële getallen én in de p-adische getallen voor elke priem p.
Re: Oneindige som
Geplaatst: ma 15 jul 2024, 17:14
door Xilvo
Ok, die macht moet een factor zijn. Ik was even op het verkeerde been gezet door 1/8 bij 12, maar ik had je correctie al gelezen dus dat is geen excuus.
Is dit equivalent:
s=1+2+4+...=1+2s
=> s=-1
?
Re: Oneindige som
Geplaatst: ma 15 jul 2024, 18:08
door Bart23
Ja, dat klopt.
Re: Oneindige som
Geplaatst: ma 15 jul 2024, 22:18
door HansH
het gaat fout in de aanname
1 + 2 ( 1 + 2 +4 + ...) = 1 + 2 S
als je S even bekijkt voor een deel van de som dan zie je het"
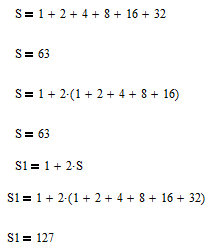
- S1 4225 keer bekeken
S zou dan gelijk moeten aan aan S1, maar zoals je ziet bevat S1 altijd 1 som meer. in het voorbeeld is dat het getal 32. terwijl als je het tussen haakjes neemt is het laatste getal maar 16.
dus S is niet gelijk aan 1+2S. Dat geldt voor n termen maar ook voor n gaande naar oneindig.
voor 6 termen zit je er dus 2^6 naast. voor oneindig termen zit je er dan 2^oneindig naast.
Re: Oneindige som
Geplaatst: ma 15 jul 2024, 22:21
door Xilvo
HansH schreef: ↑ma 15 jul 2024, 22:18
S zou dan gelijk moeten aan aan S1, maar zoals je ziet bevat S1 altijd 1 som meer. in het voorbeeld is dat het getal 32. terwijl als je het tussen haakjes neemt is het laatste getal maar 16.
Rekenen/redeneren met oneindigheden is lastig, toegegeven. Maar bij een oneindige reeks is er geen laatste term.
Re: Oneindige som
Geplaatst: ma 15 jul 2024, 22:22
door HansH
de structuur blijft hetzelfde dus dat is het bewijs. je kunt er dus steeds een term bij doen en dan zie je dat het idee precies hetzelfe blijft. dus dan is het alleen nog een kwestie van de limiet nemen naar oneindig. maar dat zijn we toch wel gewend met limieten?
Re: Oneindige som
Geplaatst: ma 15 jul 2024, 22:26
door Xilvo
HansH schreef: ↑ma 15 jul 2024, 22:22
de structuur blijft hetzelfde dus dat is het bewijs.
Bewijs het maar.
Re: Oneindige som
Geplaatst: ma 15 jul 2024, 23:12
door HansH
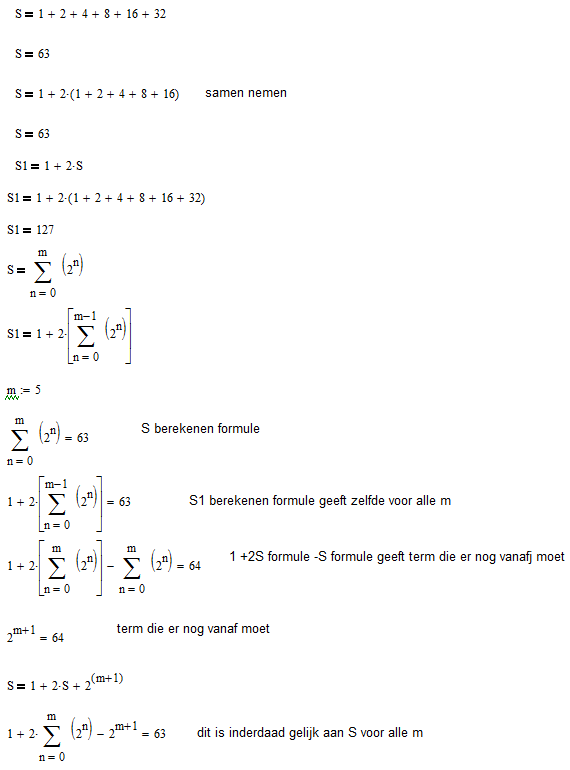
- S3 4190 keer bekeken
De afleiding laat zien dat de formule voor S gelijk is aan 1+2S+2^(m+1)
voor elke m>0 betekent het dus dat het veronderstelde verband S=1+2S niet klopt. Voor m naar oneindig maak je dan een oneindig grote fout op de uitkomst S=-1