1 van 1
stroom
Geplaatst: vr 12 jul 2024, 18:52
door ukster
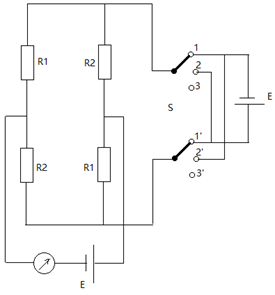
- Elektrisch circuit 4700 keer bekeken
De spanning van beide batterijen is gelijk, hun inwendige weerstand en die van de stroommeter zijn verwaarloosbaar.
Dubbelpolige schakelaar S
Stand 11’ Aanwijzing ampèremeter 6A
Stand 22’ Aanwijzing ampèremeter 3A
Stand 33’ Aanwijzing ampèremeter ??
Re: stroom
Geplaatst: vr 12 jul 2024, 19:35
door Xilvo
Ik kom op 1 A.
Re: stroom
Geplaatst: vr 12 jul 2024, 20:06
door ukster
Mijn simulatieprogramma geeft wat anders aan.
Re: stroom
Geplaatst: vr 12 jul 2024, 20:25
door Xilvo
Wel mee eens dat R1=2R2 (of omgekeerd)?
Re: stroom
Geplaatst: vr 12 jul 2024, 21:18
door ukster
R2=2R1 niet!
R1=2R2 wel
Re: stroom
Geplaatst: vr 12 jul 2024, 21:55
door Xilvo
Even zonder amperemeter (onderbroken).
Dan staat op de verbindingspunten van R1 en R2 links \(\frac{1}{3}\)E, rechts \(\frac{2}{3}\)E.
Het verschil is \(\frac{1}{3}\)E.
Die spanning wisselt van teken als je schakelt tussen stand 1 en stand 2.
Daar komt beneden nog eens E bij.
Dan heb je over de (nog afwezige) meter \(\frac{4}{3}\)E of \(\frac{2}{3}\)E. Daar heb je de factor 2 die ook voor de stroom geldt, want de inwendige weerstand van deze niet-ideale spanningsbron is, voor beide gevallen, \(\frac{R_1 R_2}{2(R_1+R_2)}\)
Met \(R_1=2R_2\) wordt dit \(\frac{1}{3}R_2\)
Schakel je naar stand 3, dan heb je alleen de spanningsbron beneden over, E.
Bij gelijkblijvende inwendige weerstand zou dit een stroom van 4,5 A opleveren, met aangesloten ampèremeter.
De inwendige weerstand wordt \((R_1+R_2)//(R_1+R_2)=\frac{1}{2}(R_1+R_2)\)
Alweer, met \(R_1=2R_2\) wordt dit \(\frac{3}{2} R_2\)
Die inwendige weerstand is \(\frac{9}{2}=4,5\) keer zo groot als bij stand 1 en 2.
De stroom wordt dus 4,5 keer zo klein, 1 A.
Re: stroom
Geplaatst: za 13 jul 2024, 00:59
door EvilBro
Waarom is het antwoord niet gewoon 4.5 A? (obv superpositie)
Re: stroom
Geplaatst: za 13 jul 2024, 09:54
door Xilvo
EvilBro schreef: ↑za 13 jul 2024, 00:59
Waarom is het antwoord niet gewoon 4.5 A? (obv superpositie)
Dat zou je krijgen als de punten 3 en 3' verbonden waren (spanningsbron met spanning nul).
Maar nu is dat een onderbreking.
Re: stroom
Geplaatst: za 13 jul 2024, 09:55
door Xilvo
ukster schreef: ↑vr 12 jul 2024, 21:18
R2=2R1 niet!
R1=2R2 wel
Inderdaad, dat "omgekeerd" wat ik eerder schreef klopt niet.
Re: stroom
Geplaatst: za 13 jul 2024, 11:51
door ukster
R1=2R2
Stel R1=2Ω,R2=1Ω
I(11')=E/R2=6A, E=6V
I(22')=E/R1=3A
I(33')=E/([R1+R2]/2)=6/1,5=4A
Re: stroom
Geplaatst: za 13 jul 2024, 14:35
door Xilvo
ukster schreef: ↑za 13 jul 2024, 11:51
R1=2R2
Stel R1=2Ω,R2=1Ω
I(11')=E/R2=6A, E=6V
I(22')=E/R1=3A
I(33')=E/([R1+R2]/2)=6/1,5=4A
De uitleg is erg summier maar je hebt gelijk. Het juiste antwoord is 4A.
Re: stroom
Geplaatst: za 13 jul 2024, 14:36
door Xilvo
Nu de correcte uitwerking:
Even zonder amperemeter (onderbroken).
Dan staat op de verbindingspunten van R1 en R2 links \(\frac{1}{3}\)E, rechts \(\frac{2}{3}\)E.
Het verschil is \(\frac{1}{3}\)E.
Die spanning wisselt van teken als je schakelt tussen stand 1 en stand 2.
Daar komt beneden nog eens E bij.
Dan heb je over de (nog afwezige) meter \(\frac{4}{3}\)E of \(\frac{2}{3}\)E. Daar heb je de factor 2 die ook voor de stroom geldt, want de inwendige weerstand van deze niet-ideale spanningsbron is, voor beide gevallen, \(2\frac{R_1 R_2}{R_1+R_2}\)
Met \(R_1=2R_2\) wordt dit \(\frac{4}{3}R_2\)
Schakel je naar stand 3, dan heb je alleen de spanningsbron beneden over, E.
Bij gelijkblijvende inwendige weerstand zou dit een stroom van 4,5 A opleveren, met aangesloten ampèremeter.
De inwendige weerstand wordt \((R_1+R_2)//(R_1+R_2)=\frac{1}{2}(R_1+R_2)\)
Alweer, met \(R_1=2R_2\) wordt dit \(\frac{3}{2} R_2\)
Die inwendige weerstand is \(\frac{9}{8}\) keer zo groot als bij stand 1 en 2.
De stroom wordt dus \(\frac{9}{8}\) keer zo klein, 4 A.