1 van 2
vierkant
Geplaatst: za 09 nov 2024, 14:20
door ukster
Vierkant met oppervlakte 1
De rechthoeken met oppervlakte A,B en C hebben dezelfde lengte/breedte verhouding.
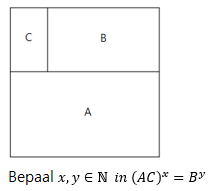
- 1 368 keer bekeken
Re: vierkant
Geplaatst: za 09 nov 2024, 14:40
door Professor Puntje
Mag de oppervlakte ook 1 m2 zijn? In dat geval heb je y = 2x .
Re: vierkant
Geplaatst: za 09 nov 2024, 14:47
door ukster
Professor Puntje schreef: ↑za 09 nov 2024, 14:40
Mag de oppervlakte ook 1 m
2 zijn? In dat geval heb je y = 2x .
ja
maar ik krijg een andere verhouding y/x
Re: vierkant
Geplaatst: za 09 nov 2024, 14:50
door Professor Puntje
Ik ben ervan uit gegaan dat dan ook de eenheden moeten kloppen.
Re: vierkant
Geplaatst: za 09 nov 2024, 15:44
door ukster
Mmm.. gezien mijn afwijkende antwoord denk ik toch meer aan een voorbeeld van schaal of verhoudingen: het zou een voorbeeld zijn van een verhouding, waarbij de oppervlakte 1 wordt gebruikt als een referentiepunt voor vergelijkingen of schaalmodellen. In deze zin kan de oppervlakte 1 niet letterlijk een eenheid zijn, maar een relatieve maat om andere oppervlakten te vergelijken.
Re: vierkant
Geplaatst: za 09 nov 2024, 16:03
door ukster
op basis hiervan
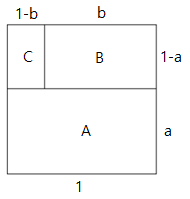
- 2 315 keer bekeken
Re: vierkant
Geplaatst: za 09 nov 2024, 16:11
door Professor Puntje
Dus: (1-b):(1-a) = (1-a):b = a:1
En dan verder wat algebra.

Re: vierkant
Geplaatst: za 09 nov 2024, 16:26
door ukster
Precies!
Re: vierkant
Geplaatst: za 09 nov 2024, 19:18
door Professor Puntje
Moeten a en b ook specifieke waarden hebben om dit mogelijk te maken?
Re: vierkant
Geplaatst: za 09 nov 2024, 19:23
door ukster
Nee, dat is hier niet nodig

Re: vierkant
Geplaatst: za 09 nov 2024, 19:26
door Professor Puntje
OK - x=y=0.
Re: vierkant
Geplaatst: za 09 nov 2024, 19:34
door ukster

- 1 263 keer bekeken
Re: vierkant
Geplaatst: za 09 nov 2024, 20:04
door Professor Puntje
Als a en b geen specifieke waarden hoeven te hebben kan ik er zelf waarden voor kiezen, dat geeft wellicht meer oplossingen dan er voor het algemene geval gelden, maar de algemeen geldige oplossingen moeten daar dan ook bij zitten. Ik kies a = 1/2 & b = 3/4.
Dan hebben we:
A = a.1 = 1/2
B = (1-a).b = 1/2 . 3/4 = 3/8
C = (1-a).(1-b) = 1/2 . 1/4 = 1/8
A.C = 1/16 = 2-4
B = 3/8 = 3.2-3
(AC)x = By
(2-4)x = (3.2-3)y
2-4x = 3y.2-3y
2-4x+3y = 3y
Maak ik hier een fout?
Edit: ze zijn niet vrij te kiezen anders kloppen de lengte en breedte verhoudingen niet...
Re: vierkant
Geplaatst: za 09 nov 2024, 20:14
door Professor Puntje
Als we a = 1/2 kiezen, moet er gelden:
(1-b):1/2 = 1/2:b = 1/2:1
2(1-b) = 1/(2b) = 1/2
En dat heeft geen oplossingen....
Re: vierkant
Geplaatst: zo 10 nov 2024, 09:53
door ukster
Professor Puntje schreef: ↑za 09 nov 2024, 19:18
Moeten a en b ook specifieke waarden hebben om dit mogelijk te maken?
Toch wel! 1 variabele is vrij te kiezen, de ander ligt dan vast (vanwege de verhouding identiteit)