sciencetalk

Hallo, ik heb een beetje een klein probleempje. Ik moet morgen mijn profielwerkstuk inleveren, en van mijn leraar moet ik er nog een bewijs inzetten van de formule van Binet.

Dat is de volgende formule:

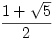Afbeelding

Ik heb al het een en ander op dit forum ervan gezien, maar dat snapte ik niet echt... (ik ben maar een simpel Havo-5'ertje....)

( http://sciencetalk.nl/forum/invision/in...dpost&pid=88170 -> die ging over Matrix-berekeningen ofzo?

en http://sciencetalk.nl/forum/invision/in...c=8853&start=12 -> Die kon ik ook neit volgen....

)

Kan iemand mij alsjeblieft helpen? Ik ben bang dat het me anders een herkansingsmogelijkheid gaat kosten.

Je bent wel nogal laat als dat pws morgen ingeleverd moet worden...

In de eerste link die je gaf, staan links naar websites met bewijzen.

Zie ook deze link of de resultaten van deze zoekopdracht met google.

Misschien kan je zeggen welk (soort) bewijs je op het oog hebt en wat je er niet aan begrijpt?

Klopt inderdaad dat ik laat ben....

Het voorzetje dat onze leraar ons had gegeven was dit:

Afbeelding

In ieder geval al bedankt voor het antwoord.

Als ik de gedachtegang van je leraar wil volgen, zou ik zeggen: bekijk de termen in a en b nu apart in die vergelijking:

\(pa^{n + 2} = pa^{n + 1} + pa^n \Leftrightarrow pa^{n + 2} - pa^{n + 1} - pa^n = 0\)

Dus:

\(pa^2 a^n - paa^n - pa^n = 0 \Leftrightarrow pa^n \left( {a^2 - a - 1} \right) = 0\)

Okay.... Volgens mij bedoelde hij dat inderdaad ja... bedankt!

Maar zo kan ik dus a berekenen, wat het getal Phi (

\( \frac{1+\sqrt{5}}{2}\)

) wordt...

Maar als ik op dezelfde manier b wil berekenen, dan krijg ik daar toch weer Phi uit als antwoord? En geen Phi-1 (

\( \frac{1-\sqrt{5}}{2}\)

), wat het wel zo zou moeten zijn....

Heeft een kwadratische vergelijking (als de discriminant positief is...) niet twee oplossingen?

Ja dat klopt... Maar waarom moet ik voor a Afbeelding

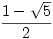en voor b, de andere uitkomst van de kwadratische vergelijking nemen? ( Afbeelding

dus)?

In het begin heb je de twee onbekenden a en b genoemd, maar deze zijn natuurlijk onderling verwisselbaar.

Misschien komt het door het tijdstip, misschien doordat ik gewoon dom ben... Maar hoe kom ik dan aan p of q?

btw, ik heb nu alleen dit nog maar als uitleg... Maar die is dus nog niet af....

Uit de voorwaarde u(0) = 0 heb je al dat p+q = 0.

Maar er is een tweede beginwaarde, namelijk u(1) = 1.

Daaruit volgt de voorwaarde:

\(u\left( 1 \right) = 1 \Rightarrow p\left( {\frac{{1 + \sqrt 5 }}{2}} \right) + q\left( {\frac{{1 - \sqrt 5 }}{2}} \right) = 1\)

Vervang q door -p en los op naar p, je vind 1/sqrt(5). Dan is q het tegengestelde.

FlorianK schreef:Toch doe ik iets fout....

Dat komt omdat je (oorspronkelijke) formule fout is, er moet niet 5 maar [wortel]5 in de noemer.

Edit: je hebt je berichtje blijkbaar verwijderd...

Ik was achter mijn fout gekomen ja...

Nu heb ik dit als uitleg.

Ik heb hem nu bewezen dacht ik... Ik vraag me alleen nog af of mijn leraar niet een stukje tekst of uitleg mist, daar waar ik die bruine streep heb neergezet?

In ieder geval: Heel erg hartelijk bedankt!

Dat zou goed kunnen, maar ik weet niet wat je leraar in gedachte had voor de methode waarvan hij alleen de aanzet gaf...

Het kan minder moeizaam door eerst aan te tonen (met volledige inductie) dat

\(\phi_i^n = F_n \phi_i + F_{n-1}\)

Hierbij is \((F_n)\) het rijtje van Fibonacci en \(\phi_i = \phi_1 \mbox{ of } \phi_i=\phi_2\).

\(\phi_1 = \frac{1+\sqrt{5}}{2} \mbox{ en } \phi_2 = \frac{1-\sqrt{5}}{2}\)

zijn de nulpunten van \(\phi^2 = 1 + \phi\).

Dan is

\(\frac{\phi_1^n - \phi_2^n}{\phi_1 - \phi_2} = F_n\)

Uit een werkstukje van mij van enkele jaren terug:

Vind alle mogelijke rijen die voldoen aan

\((u_n)_{\nin\mathbb{N}}:u_{n+1}=u_n+u_{n-1}\)

. Wat heeft dit te maken met

\(\phi=\frac{1+\sqrt5}{2}\)

?

Beschouw

\(V={(u_n)_{\nin\mathbb{N}}|u_{n+1}=u_n+u_{n-1}}\)

. Het is eenvoudig

na te gaan dat

\(\mathbb{R},V,+\)

een vectorruimte is. Een eenvoudige

basis van

\(V\)

is

\(\beta={(0,1,1,2,3,5,\ldots),(1,1,2,3,5,8,\ldots)}\)

. Met

\(\beta\)

zelf zijn we niet bijster veel, maar we weten nu wel dat twee

lineair onafhankelijke rijen uit

\(V\)

steeds een basis voor

\(V\)

vormen. Stel nu

\(r=\frac{1+\sqrt5}{2}\)

en

\(s=\frac{1-\sqrt5}{2}\)

.

Omdat

\(r\neq s\)

geldt dat de rijen

\((a_n)_{\nin\mathbb{N}}=(1, r, r+1, \ldots)\)

\((b_n)_{\nin\mathbb{N}}=(1, s, s+1, \ldots)\)

een basis voor

\(V\)

vormen. Uit het voorgaande weten we echter dat

\(r^2=r+1\)

,

\(r^3=r^2+r\)

,

\(r^4=r^3+r^2\)

, enzovoort (analoog voor

\(s\)

).

Dus de meetkundige rijen

\((a_n)_{\nin\mathbb{N}}:a_n=r^n\)

en

\((b_n)_{\nin\mathbb{N}}:b_n=s^n\)

vormen een basis voor

\(V\)

. We

besluiten dus dat

\(\forall(u_n)_{\nin\mathbb{N}}\inV:\exists\lambda,\mu\in\mathbb{R}:\forall \nin\mathbb{N}:u_n=\lambdar^n+\mu s^n\)

Dit laat ons toe om op een gemakkelijke

manier een expliciet voorschrift te vinden voor een

\((u_n)_{\nin\mathbb{N}}\in V\)

. Kies bijvoorbeeld de rij van

Fibonacci. Omdat

\(f_0=f_1=1\)

geeft de kwantorenuitspraak aanleiding tot het stelsel

\(\left{ \begin{array}{\ll} \lambda+\mu=1\lambda r+\mu s=1\end{array} \right.\sim\left{ \begin{array}{\ll} \lambda=\frac{1-s}{r-s}=\frac{\sqrt5}{10}+\frac{1}{2}\mu=\frac{r-1}{r-s}=\frac{1}{2}-\frac{\sqrt5}{10}.\end{array} \right.\)

Dit strookt inderdaad met de formule van Binet.

Het kan zijn dat je hier en daar een indexje moet aanpassen, maar het idee is volgens mij juist.

N.D.

sciencetalk

Formule van Binet bewijzen

Formule van Binet bewijzen

Re: Formule van Binet bewijzen

Re: Formule van Binet bewijzen

Re: Formule van Binet bewijzen

Re: Formule van Binet bewijzen

Re: Formule van Binet bewijzen

Re: Formule van Binet bewijzen

Re: Formule van Binet bewijzen

Re: Formule van Binet bewijzen

Re: Formule van Binet bewijzen

Re: Formule van Binet bewijzen

Re: Formule van Binet bewijzen

Re: Formule van Binet bewijzen

Re: Formule van Binet bewijzen

Re: Formule van Binet bewijzen