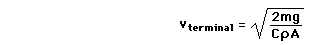sciencetalk

Als men nu 2 voorwerpen van dezelfde hoogte, en op hetzelfde moment, loslaat. Beide voorwerpen zijn even groot maar de massa is verschillend. Welk voorwerp zal het eerst de grond bereiken(mits wrijving met de lucht)?

Ik denk het zware object, omdat dit object meer impuls ontwikkeld (m*v) en daardoor de lucht makkelijker doorklieft.

Als de voorwerpen dezefde vorm hebben, hebben ze dan ook ni evenveel wrijving bij naar beneden vallen? K weet dat het op een horizontaal oppervlak niet zo is, maar dat heeft denk ik dan met het contact tussen de oppervlakten te maken en bij vrije val lijkt mij dat minder logisch...

Een verdere onderbouwing van mijn antwoord!

Omdat de kogel naar beneden valt zal het de lucht (relatief gezien) netto omhoog zien gaan, als de lucht thermodynamisch in rust is (geen wind ofzo) De kogel botst met deeltjes die gemiddeld gezien omhoog gaan.

Bij deze botsingen (stel ze zijn compleet elastisch, al maakt dat heir niet uit) geldt natuurlijk het behoud van impuls (m*v).

Voor de botsing: Bal valt naar beneden deeltje gaat omhoog

Na de botsing: Bal valt iets langzamer naar beneden en deeltje gaat omlaag.

Tijdens de overdracht heeft de neerwaardse impuls van de kogel twee keer de originele impuls (die naar boven gericht is ) moeten betalen. Absoluut gezien is dit even groot, maar de lichtere kogel wordt meer afgeremd, omdat het minder massa heeft en dezelfde impulsafname zorgt voor een grotere snelheidsafname en dus zal de lichte kogel de grond later raken dan de zware

De bovenstaande antwoorden kloppen allemaal niet. De massa van de voorwerpen is totaal (bewijsbaar) niet van belang. Alleen de wrijving speelt een rol. In vacuum valt een veertje van een vogel dus exact even snel als een hamer. Dit is experimenteel vaak bewezen, onder andere door Neil Armstrong toen hij op de maan stond. Overigens is dit experiment reeds door Galileo gedaan: LINK.

-Freek.

mits wrijving met de lucht

Natuurlijk valt alles in vacuum even snel, maar dat wordt hier niet gevraagd!

Zie een veer en een hamer in je eigen zolderkamer

Of relevanter: een leeg pingpongballetje en een gevult met water!

Originele vraag:

[...]Beide voorwerpen zijn even groot maar de massa is verschillend.

jouw originele vraag is niet volledig. Je moet wrijving in beschouwing nemen.

De massa maakt inderdaad niet uit nee. Het volume anders wel. Ik herinner me een energiebalans van natuurkunde van de havo. De wet van behoud van energie geloof ik. Hierin stonden aan twee kanten van het = teken massas (deze kwamen geloof ik in alle termen voor (o.a kinetische energie (0,5mv^2 en potentiele energie mgh) en daarom kon je die wegstrepen, dus massa doet er niet toe.

Maar hoe groter het volume ja, des te meer wrijving, dus volgens mij des te langer het duurt voordat het voorwerp op de grond komt.

Niet helemaal, het is belangrijker hoe groot het oppervlak is dat naar de grond is gericht. Eigelijk is de vorm dus heel belangrijk. Als je turbulentie creeert vertraagd dat namelijk de snelheid. (entropie wordt wel groter, door wrijving)

OK, ik heb het even uitgezocht. We hebben allemaal een beetje gelijk!

Als het deeltje net begint met vallen, dan is de wrijvingskracht evenredig met de snelheid van het vallende deeltje. In dit geval valt de massa er prachtig uit en krijg je het resultaat van Galileo; dat het alleen uitmaakt wat de vorm van het deeltje is.

Als het deeltje echter al wat langer valt, dan begint deze zijn 'eindsnelheid' te bereiken. (Ook als een object heel lang zou vallen in een medium, dan nog wordt zijn snelheid niet steeds groter; er is een limiet. Deze limiet heet de eindsnelheid of 'terminal velosity' en is bijvoorbeeld voor een mens in vrije val zo'n 300 km/h.) In dit gebied is de wrijvingskracht evenredig met het kwadraat van de snelheid van het vallende deeltje. In dit geval valt de massa er niet uit, maar krijg je iets dat afhangt van de wortel van de massa. In dit geval zal er dus wel een verschil ontstaan in valsnelheid tussen twee gelijkvormige objecten van verschillende massa.

In de praktijk zitten we echter meestal in het eerste geval en dus kan je de massa negeren. Meestal kan je zelfs ook de vorm van het object negeren! Doe maar eens een experiment met een druif en een sinasappel: als je ze tegelijk van gelijke hoogte laat vallen, dan komen ze gelijk neer.

-Freek.

voor alle mensen die denken dat de vorm van het voorwerp er niet toe doet: Ik spring uit een vliegtuig met een parachute de andere zonder. Rarara wie is er het eerst beneden.

zwaartekracht:

Fz = mg

benadering van wrijvingskracht:

Fw = a*v^2

met a een constante die niet afhangt van de massa, maar wel van bijvoorbeeld de vorm van het object en het medium bijvoorbeeld lucht.

resulterende kracht:

F = m.a = mg-a*v^2

a= g- (a.v^2)/m

het voorwerp met de grootste massa, heeft relatief de grootste versnelling

v=a.t

en dus ook de grootste snelheid..

bij twee objecten met zelfde geometrie maar andere massa, zal de zwaardere eerder beneden zijn.

Groet, Gijs

Klopt, als je de kracht dus kwadratisch in de snelheid kiest,



(rho = dichtheid, A = oppervlak van vallend object, C = drag-coefficient en v=snelheid)

dan vind je dus voor de netto-kracht dat



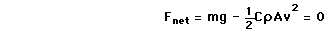
en deze moet 0 zijn in de stabiele limiet (terminal velosity).

De uiteindelijke snelheid is dan dus



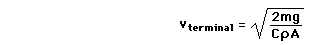
evenredig met de wortel van de massa.

Dit effect is echter meestal vrij klein:

Honkbal-bal (3.66 cm radius, 145 g, A = 42 cm^2) --> v_t = 33 m/s

Golf-bal (2.1 cm radius, 46 g, A = 14 cm^2) --> v_t = 32 m/s

Hier kan je zelf wat getallen invullen in een javascript programmatje en dan kijken wat voor een v_t je krijgt.

Alleen bij heel grote massa-verschillen en/of heel grote oppervlak-verschillen krijg je echt een groot effect. Bijvoorbeeld een opgeblazen balon valt echt heel erg veel langzamer dan een bowlingbal...

Overigens is het natuurlijk zo dat dit effect pas belangrijk wordt als het vallende object al een significante snelheid heeft. Zolang de gravitatieversnelling (veel) groter is dan f_drag, zullen alle objecten met gelijke versnelling vallen. Aangezien de meeste vrije vallen kort zijn, verklaart dit ook waarom Galileo nooit een effect van de massa in zijn valexperimenten heeft waargenomen.

-Freek.

Als het in een vacuum ruimte is, dan raken ze tegelijk de grond, maar als het niet in een vacuum ruimte is, dan is het zwaarste voorwerp eerder aan de grond.