1 van 1
Optimalisatie oefening
Geplaatst: zo 22 apr 2007, 11:58
door raintjah
Hey,
ik kan om de één of andere reden totaal niet beginnen aan de volgende oefening.. Een aanzet is dus meer dan welkom.
Beschouw een eindige verzameling punten \((x_i,y_i,z_i)\)
in

³ (i=1,...,n). Vind a,b,c in

zodat het vlak in

³ met vergelijking z=ax+by+c het best aansluit bij deze punten in die zin dat
\(\sum_{i=1}^n (ax_i+by_i+c-z_i)^2\)
minimaal is.[/size]
Wie kan mij op weg helpen? Ik denk dat ik de meetkundige betekenis van de opgave niet zie...
Alvast bedankt!
Stijn
EDIT: Dit staat hier fout, het moet onder analyse staan. Was ondertussen al zo gewend in dit subforum te posten..
Mijn excuses

Re: Optimalisatie oefening
Geplaatst: zo 22 apr 2007, 12:06
door PeterPan
Je kun door haakjes uit te werken
\(\sum_{i=1}^n (ax_i+by_i+c-z_i)^2\)
schrijven in de vorm
\((a,b,c,1) \mbox{ (4x4 matrix) }(a,b,c,1)^T\)
Re: Optimalisatie oefening
Geplaatst: zo 22 apr 2007, 12:17
door raintjah
Nog altijd geen flauw idee hoe ik daaruit moet minimaliseren...

Re: Optimalisatie oefening
Geplaatst: zo 22 apr 2007, 12:19
door PeterPan
differentieren naar a en nul stellen.
differentieren naar b en nul stellen.
differentieren naar c en nul stellen.
Re: Optimalisatie oefening
Geplaatst: zo 22 apr 2007, 12:24
door Brinx
Even over de meetkundige betekenis van je opgave: het is een geval waarin je een plat vlak door een verzameling (3D) punten probeert te leggen zodat de absolute hoogte-fout (de z-waarde) voor alle punten samen zo klein mogelijk is: je maakt hierbij gebruik van de 'kleinste kwadraten methode' (least squares method). Hieronder een schets met een analoog geval, in 2D:
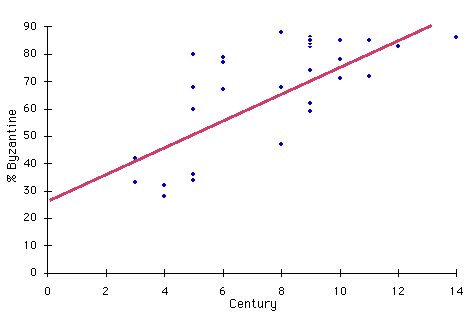
(bron:
http://www.skypoint.com/members/waltzmn/Le...quaresChart.GIF )
Hier zie je dat er een rechte lijn is getrokken door een verzameling punten in het platte vlak. De lijn is zo gekozen dat de som van de kwadraten van alle verticale afstanden van de punten tot de lijn zo klein mogelijk is. PeterPan gaf al een hint over hoe je zoiets concreet uit kunt rekenen - een hele berg informatie is op internet te vinden als je googlet (googelt?) op 'kleinste kwadraten' of 'least squares'.
Re: Optimalisatie oefening
Geplaatst: zo 22 apr 2007, 12:40
door raintjah
Oké, straks nog een proberen, alvast bedankt PeterPan en Brinx!
OFFTOPIC:
http://www.mijnwoordenboek.nl/werkwoord/googelen
Re: Optimalisatie oefening
Geplaatst: zo 22 apr 2007, 14:19
door raintjah
Stel even dat
\(F:\rr^3 \rightarrow \rr^+ : (a,b,c) \mapsto \sum_{i=1}^n (ax_i+by_i+c-z_i)^2\)
, is dan
\(D_1F(a,b,c) = \sum_{i=1}^n2(ax_i+by_i+c-z_i)x_i\)
?
Re: Optimalisatie oefening
Geplaatst: ma 23 apr 2007, 18:02
door raintjah
Klopt dat?
Re: Optimalisatie oefening
Geplaatst: ma 23 apr 2007, 18:26
door PeterPan
Klopt dat?
hartstikke, en
\(D_1F(a,b,c) = \sum_{i=1}^n2(ax_i+by_i+c-z_i)x_i = a.2.\sum_{i=1}^nx_i^2 +b.2.\sum_{i=1}^ny_ix_i +c.2.\sum_{i=1}^nx_i + 2.\sum_{i=1}^nz_ix_i \)
.

³ (i=1,...,n). Vind a,b,c in
zodat het vlak in
³ met vergelijking z=ax+by+c het best aansluit bij deze punten in die zin dat
\(\sum_{i=1}^n (ax_i+by_i+c-z_i)^2\)minimaal is.[/size]