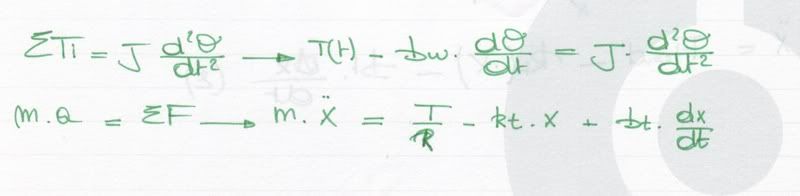Transfertfunctie zoeken
Geplaatst: za 11 aug 2007, 13:29
hello,
ik heb hier een oefening waar ik de transfertfunctie moet zoeken. Maar ik zit al vast om de differentiaalvergelijkingen te zoeken, kan iemand me helpen??
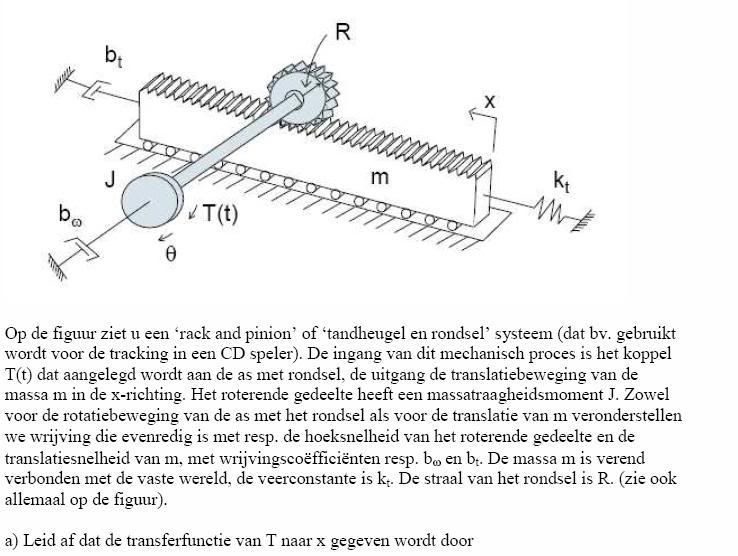
Tis vooral wat ik met dat tandwiel moet doen waar ik last mee heb.
alvast bedankt
ik heb hier een oefening waar ik de transfertfunctie moet zoeken. Maar ik zit al vast om de differentiaalvergelijkingen te zoeken, kan iemand me helpen??

Tis vooral wat ik met dat tandwiel moet doen waar ik last mee heb.
alvast bedankt