[microcursus] ruimte-tijd: een voorstelling
Geplaatst: ma 28 mei 2007, 11:15
Er is ook een volledig overzicht van alle cursussen, FAQ's en handleidingen .
Als je van deze cursus gebruik maakt, willen we je vriendelijk vragen te laten weten wat je er van vond:
---------------------------------------------------------------------------------------
RUIMTE-TIJD: een voorstelling
Auteur: Rogier
In discussies over het ontstaan van de ruimte, de vraag of het heelal oneindig is, het begin van de tijd, enzovoort, lopen mensen soms stuk met een aantal lastige vragen. Zoals:
Vergelijk ons universum met een tekenfilm. We hebben het dan over een 2-dimensionaal heelal (een vel papier) dat verandert in de tijd, een 3-dimensionale ruimtetijd dus. Een tekenfilmfiguur beleeft zijn 2D wereld als eindig, want er is maar een eindige hoeveelheid papier oppervlakte, en er zitten randen of grenzen aan:

Als hij dus naar boven of onder of links of rechts loopt, komt hij een rand tegen.
Stel nou dat je het papier rond vouwt en er een koker (cilinder) van maakt. Donald merkt dat niet in zijn 2D wereld, want wat voor ons gebogen of "krom" is, is voor hem nog steeds rechtdoor. Die kromming is in een richting die hij niet kent of ervaart. Hij zit nog steeds in z'n platte wereldje en kent alleen boven/onder en links/rechts. Maar hij kan nu wel altijd in één richting (links/rechts) blijven doorlopen, de cylinder rond, en weer op hetzelfde punt uitkomen:
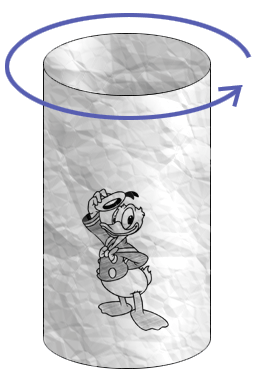
Boven en onder is er voor hem nog wel een rand.
Als je dat rondvouwen niet in één richting doet, maar in twee richtingen, dus dan maak je er een (holle) papieren bol van in plaats van een cilinder, dan komt onze gevederde vriend nooit meer ergens een "grens" (rand van het papier) tegen. Terwijl z'n papieren oppervlak nog steeds net zo groot (eindig) is:
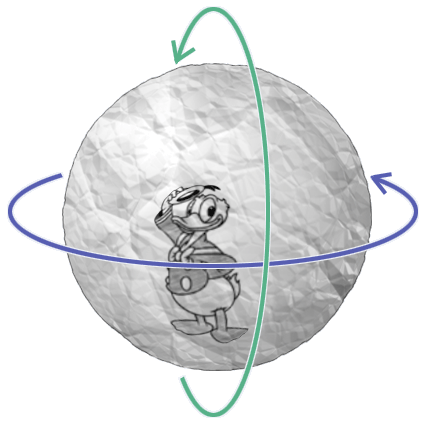
Beeld je alvast even in hoe dit voor Donald moet zijn: hij zit in een platte, 2-dimensionale wereld (dingen in 3D kan hij zich helemaal niet voorstellen), die wereld heeft een eindige grootte (bijvoorbeeld de oppervlakte van een A4'tje) en toch komt hij nergens een rand tegen, hoe ver hij ook loopt! Wij als 3D-denkende mensen kunnen natuurlijk zien dat dat komt omdat zijn platte wereld tot een boloppervlak is gevouwen, maar stel je even voor hoe raadselachtig dit moet zijn vanuit zijn perspectief.
Bedenk ook dat het hier een belangrijk verschil maakt dat wij mensen weliswaar ook op een bol rondlopen (de aarde), maar dat wij er loodrecht op staan en omhoog kunnen kijken, terwijl Donald echt op (of in) het papier zit.
Nou heb je heel veel frames van de tekenfilm. Verschillende frames achter elkaar is eigenlijk het verstrijken van tijd voor Donald, het ene frame stelt in de tekenfilmtijd een ander moment voor dan een ander frame. Voor Donald volgen de frames elkaar in de tijd op. Stel nou dat je de eerste frames heel klein maakt en hoe verder (later) je bent in de tekenfilm, hoe groter de vellen papier.
En alle velletjes zijn tot een bol gevouwen, beginnend met kleine bolletjes, en steeds groter:
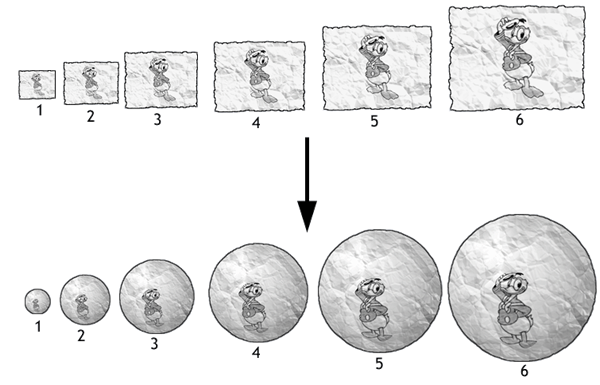
En die stop je allemaal in elkaar, net zoals van die poppetjes vroeger die je open kon maken en dan zat er een kleiner poppetje in, enzovoort. Dan krijg je een soort massieve papieren klomp, waarbij de lagen of "schillen" van de bol ieder een frame (moment in de tijd) zijn. Beetje lastig om te tekenen, maar dit moet hem voorstellen als je het hele ding doormidden zou zagen:

Misschien moeilijk te zien, maar hier kijk je in een gehalveerde holle bol, die in andere bollen ligt. Er zitten dus kleine papieren bollen in grotere.
Het hele object is nu de complete ruimtetijd van de tekenfilm, en de tijd is de richting van het centrum van de bol naar buiten. De kleine frames dicht bij het midden van de bol komen (in de tijdsbeleving van Donald) eerder dan de grotere frames verder weg.
Wat hebben we hiermee: een 2D universum...
Zoals je ziet heeft het universum geen middelpunt dat Donald binnen de 2D "ruimte" waarin hij leeft kan aanwijzen. Het centrum van de bol is niet het midden van Donald's 2D heelal: al die laagjes papier zijn namelijk ieder op zich datzelfde 2D heelal, op verschillende momenten. En ieder van die momentopnamen van het universum heeft geen eigen middelpunt - althans geen middelpunt dat op het betreffende laagje papier van dat moment.
Het middelpunt van Donald's universum bevindt zich namelijk ergens anders, buiten dat laagje papier, in het midden van alle bollen tegelijkertijd. En dat zou Donald alleen maar kunnen zien als hij in de 3e dimensie van zijn universum zou kunnen kijken. Die 3e dimensie is in het geval van Donald de tijd, zijn wereld omvat immers één ruimtelijke dimensie minder. Voor ons (met drie ruimtelijke dimensies) is de tijd de 4e dimensie. Donald kan, net zoals wij, niet buiten de ruimtelijke dimensies kijken. Hij kan immers niet in heden en verleden tegelijkertijd aanwezig zijn, of het verleden zien. Zijn "ruimte" is, op elk afzonderlijk moment in de tijd, beperkt tot zijn 2 ruimtelijke dimensies.
Net als bij ons, ligt het midden van het universum in het verleden!
Bovendien is de vraag wat er om het heelal heen zat toen het klein begon en groter werd, niet van toepassing. Of je zou kunnen zeggen dat de toekomst er omheen zat. Maar er is niet een grote lege ruimte waarin het heelal een klein stukje was, en binnen die grote lege ruimte steeds groter werd. De ruimte zelf was in het begin heel klein, en wordt met het verstrijken van de tijd in alle richtingen groter. De richting waarin die uitzetting plaatsvindt (naar buiten toe) is eigenlijk de tijd, wat voor Donald de 3e dimensie is, en voor ons de 4e. En die staat loodrecht op de ruimte, en die richting kun je binnen het universum niet ervaren of aanwijzen.
Als Donald zich op een bepaald moment afvraagt waar de big bang heeft plaatsgevonden, is het antwoord: overal. Zijn héle ruimte (het laagje papier) was namelijk ooit het kleine punt in het midden wat is uitgedijd tot de grote bol van dat moment.
Tel nu overal één dimensie bij op, dus met een 3-dimensionale ruimte in plaats van een 2-dimensionaal oppervlak, en je hebt de uitleg voor ons eigen heelal. Dit klinkt misschien als een te simpele voorstelling van zaken, maar dat komt omdat we moeite hebben met "4D denken" (net zoals Donald moeite heeft met 3D denken). Wiskundig is het precies hetzelfde. Merk op dat ik geen extra dimensies "erbij haal" ten opzichte van de normale ruimtetijd, waar we (zonder erbij stil te staan) eigenlijk altijd al vanuit gaan. Mijn hele ruimtetijd-model is 4-dimensionaal, net zoals alle andere modellen die uitgaan van 3 ruimtelijke en 1 tijdsdimensie.
Eventuele extra dimensies die volgen uit snaar-, M-theorie of TOE's, vormen (voor zover ik een snars van die theorieën heb begrepen) geen tegenspraak met mijn model hierboven.
Merk op dat zo'n (hyper)bolvormig universum slechts één mogelijke voorstelling is van de situatie, er zijn ingewikkeldere constructies mogelijk. Er is nog weinig bekend over de geometrische structuur van het heelal. Bovenstaande voorstelling is dus niet zaligmakend, maar kan worden gebruikt als denkwijze om je bij een aantal lastige zaken (zoals bijvoorbeeld de vragen aan het begin van dit verhaal) een oplossing voor te kunnen stellen.
Als je van deze cursus gebruik maakt, willen we je vriendelijk vragen te laten weten wat je er van vond:
- Geef eventuele foutjes aan;
- Zijn de onderdelen soms onduidelijk, of net erg helder?
- Ontbreken er volgens jou stukken, of heb je suggesties?
- ...
---------------------------------------------------------------------------------------
RUIMTE-TIJD: een voorstelling
Auteur: Rogier
In discussies over het ontstaan van de ruimte, de vraag of het heelal oneindig is, het begin van de tijd, enzovoort, lopen mensen soms stuk met een aantal lastige vragen. Zoals:
- Hoe het kan dat het universum een eindige grootte heeft, maar geen rand?
- Hoe kan het dat de tijd een begin heeft, en waarom is er geen "daarvoor"?
- Wat zat er om de ruimte heen toen het als klein universumpje begon en ging uitzetten?
- Waarom heeft het universum geen middelpunt?
- Op welke plek in de ruimte heeft de big bang plaatsgevonden?
Vergelijk ons universum met een tekenfilm. We hebben het dan over een 2-dimensionaal heelal (een vel papier) dat verandert in de tijd, een 3-dimensionale ruimtetijd dus. Een tekenfilmfiguur beleeft zijn 2D wereld als eindig, want er is maar een eindige hoeveelheid papier oppervlakte, en er zitten randen of grenzen aan:

Als hij dus naar boven of onder of links of rechts loopt, komt hij een rand tegen.
Stel nou dat je het papier rond vouwt en er een koker (cilinder) van maakt. Donald merkt dat niet in zijn 2D wereld, want wat voor ons gebogen of "krom" is, is voor hem nog steeds rechtdoor. Die kromming is in een richting die hij niet kent of ervaart. Hij zit nog steeds in z'n platte wereldje en kent alleen boven/onder en links/rechts. Maar hij kan nu wel altijd in één richting (links/rechts) blijven doorlopen, de cylinder rond, en weer op hetzelfde punt uitkomen:

Boven en onder is er voor hem nog wel een rand.
Als je dat rondvouwen niet in één richting doet, maar in twee richtingen, dus dan maak je er een (holle) papieren bol van in plaats van een cilinder, dan komt onze gevederde vriend nooit meer ergens een "grens" (rand van het papier) tegen. Terwijl z'n papieren oppervlak nog steeds net zo groot (eindig) is:

Beeld je alvast even in hoe dit voor Donald moet zijn: hij zit in een platte, 2-dimensionale wereld (dingen in 3D kan hij zich helemaal niet voorstellen), die wereld heeft een eindige grootte (bijvoorbeeld de oppervlakte van een A4'tje) en toch komt hij nergens een rand tegen, hoe ver hij ook loopt! Wij als 3D-denkende mensen kunnen natuurlijk zien dat dat komt omdat zijn platte wereld tot een boloppervlak is gevouwen, maar stel je even voor hoe raadselachtig dit moet zijn vanuit zijn perspectief.
Bedenk ook dat het hier een belangrijk verschil maakt dat wij mensen weliswaar ook op een bol rondlopen (de aarde), maar dat wij er loodrecht op staan en omhoog kunnen kijken, terwijl Donald echt op (of in) het papier zit.
Nou heb je heel veel frames van de tekenfilm. Verschillende frames achter elkaar is eigenlijk het verstrijken van tijd voor Donald, het ene frame stelt in de tekenfilmtijd een ander moment voor dan een ander frame. Voor Donald volgen de frames elkaar in de tijd op. Stel nou dat je de eerste frames heel klein maakt en hoe verder (later) je bent in de tekenfilm, hoe groter de vellen papier.
En alle velletjes zijn tot een bol gevouwen, beginnend met kleine bolletjes, en steeds groter:

En die stop je allemaal in elkaar, net zoals van die poppetjes vroeger die je open kon maken en dan zat er een kleiner poppetje in, enzovoort. Dan krijg je een soort massieve papieren klomp, waarbij de lagen of "schillen" van de bol ieder een frame (moment in de tijd) zijn. Beetje lastig om te tekenen, maar dit moet hem voorstellen als je het hele ding doormidden zou zagen:

Misschien moeilijk te zien, maar hier kijk je in een gehalveerde holle bol, die in andere bollen ligt. Er zitten dus kleine papieren bollen in grotere.
Het hele object is nu de complete ruimtetijd van de tekenfilm, en de tijd is de richting van het centrum van de bol naar buiten. De kleine frames dicht bij het midden van de bol komen (in de tijdsbeleving van Donald) eerder dan de grotere frames verder weg.
Wat hebben we hiermee: een 2D universum...
- dat verandert in de tijd (want op elk frame staat een ander plaatje)
- dat eindig qua grootte maar wel onbegrensd is
- dat op tijdstip 0 begint als een singulariteit (een oneindig klein punt)
- waar per definitie geen moment vóór "het begin" bestaat
- dat met het verloop der tijd uitzet in alle richtingen
Zoals je ziet heeft het universum geen middelpunt dat Donald binnen de 2D "ruimte" waarin hij leeft kan aanwijzen. Het centrum van de bol is niet het midden van Donald's 2D heelal: al die laagjes papier zijn namelijk ieder op zich datzelfde 2D heelal, op verschillende momenten. En ieder van die momentopnamen van het universum heeft geen eigen middelpunt - althans geen middelpunt dat op het betreffende laagje papier van dat moment.
Het middelpunt van Donald's universum bevindt zich namelijk ergens anders, buiten dat laagje papier, in het midden van alle bollen tegelijkertijd. En dat zou Donald alleen maar kunnen zien als hij in de 3e dimensie van zijn universum zou kunnen kijken. Die 3e dimensie is in het geval van Donald de tijd, zijn wereld omvat immers één ruimtelijke dimensie minder. Voor ons (met drie ruimtelijke dimensies) is de tijd de 4e dimensie. Donald kan, net zoals wij, niet buiten de ruimtelijke dimensies kijken. Hij kan immers niet in heden en verleden tegelijkertijd aanwezig zijn, of het verleden zien. Zijn "ruimte" is, op elk afzonderlijk moment in de tijd, beperkt tot zijn 2 ruimtelijke dimensies.
Net als bij ons, ligt het midden van het universum in het verleden!
Bovendien is de vraag wat er om het heelal heen zat toen het klein begon en groter werd, niet van toepassing. Of je zou kunnen zeggen dat de toekomst er omheen zat. Maar er is niet een grote lege ruimte waarin het heelal een klein stukje was, en binnen die grote lege ruimte steeds groter werd. De ruimte zelf was in het begin heel klein, en wordt met het verstrijken van de tijd in alle richtingen groter. De richting waarin die uitzetting plaatsvindt (naar buiten toe) is eigenlijk de tijd, wat voor Donald de 3e dimensie is, en voor ons de 4e. En die staat loodrecht op de ruimte, en die richting kun je binnen het universum niet ervaren of aanwijzen.
Als Donald zich op een bepaald moment afvraagt waar de big bang heeft plaatsgevonden, is het antwoord: overal. Zijn héle ruimte (het laagje papier) was namelijk ooit het kleine punt in het midden wat is uitgedijd tot de grote bol van dat moment.
Tel nu overal één dimensie bij op, dus met een 3-dimensionale ruimte in plaats van een 2-dimensionaal oppervlak, en je hebt de uitleg voor ons eigen heelal. Dit klinkt misschien als een te simpele voorstelling van zaken, maar dat komt omdat we moeite hebben met "4D denken" (net zoals Donald moeite heeft met 3D denken). Wiskundig is het precies hetzelfde. Merk op dat ik geen extra dimensies "erbij haal" ten opzichte van de normale ruimtetijd, waar we (zonder erbij stil te staan) eigenlijk altijd al vanuit gaan. Mijn hele ruimtetijd-model is 4-dimensionaal, net zoals alle andere modellen die uitgaan van 3 ruimtelijke en 1 tijdsdimensie.
Eventuele extra dimensies die volgen uit snaar-, M-theorie of TOE's, vormen (voor zover ik een snars van die theorieën heb begrepen) geen tegenspraak met mijn model hierboven.
Merk op dat zo'n (hyper)bolvormig universum slechts één mogelijke voorstelling is van de situatie, er zijn ingewikkeldere constructies mogelijk. Er is nog weinig bekend over de geometrische structuur van het heelal. Bovenstaande voorstelling is dus niet zaligmakend, maar kan worden gebruikt als denkwijze om je bij een aantal lastige zaken (zoals bijvoorbeeld de vragen aan het begin van dit verhaal) een oplossing voor te kunnen stellen.