Van poolco
Geplaatst: zo 16 mar 2008, 06:34
Ik wist niet of dit meer sterrenkunde of wiskunde is, maar het leek mij hier wel passen. Zoniet, verplaats hem gerust.
Ik heb dus de poolcoördinaten van de planeet uitgerekend, met de zon als oorsprong en als x-as het gestreepte lijntje van de zon richting punt P. In het plaatje onder is die slechts gedeeltelijk getekend (volledige pagina hier)
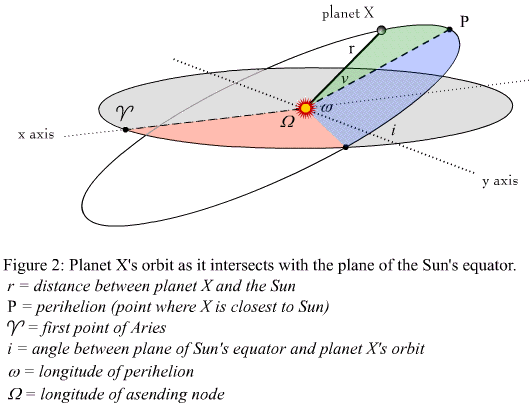
Nu moet ik deze poolcoördinaten omzetten naar zogenaamde heliocentrische ecliptische coördinaten. Om dat te doen moet ik ze eerst omzetten naar cartetische coördinaten en dan het referentievlak verschuiven zodat de x-as richting
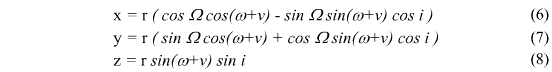
De werkwijze ontgaat mij echter volledig. Zou iemand een kleine uitleg kunnen geven hoe je stapsgewijs tot die vergelijking komt? Als ik weet hoe je tot de vergelijking van
Ik heb dus de poolcoördinaten van de planeet uitgerekend, met de zon als oorsprong en als x-as het gestreepte lijntje van de zon richting punt P. In het plaatje onder is die slechts gedeeltelijk getekend (volledige pagina hier)

Nu moet ik deze poolcoördinaten omzetten naar zogenaamde heliocentrische ecliptische coördinaten. Om dat te doen moet ik ze eerst omzetten naar cartetische coördinaten en dan het referentievlak verschuiven zodat de x-as richting
\(\Upsilon\)
wijst. Dat eerste is simpel, maar ik zie niet hoe je het tweede klaar kunt spelen. Dit is in ieder geval het antwoord: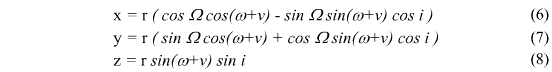
De werkwijze ontgaat mij echter volledig. Zou iemand een kleine uitleg kunnen geven hoe je stapsgewijs tot die vergelijking komt? Als ik weet hoe je tot de vergelijking van
\(x\)
komt dan kan ik de andere twee ook wel uitvogelen denk ik.