sciencetalk

Kan iemand mij uit de nood helpen bij de volgende vraagjes:

1)Geg: r=2cm

Hoe ver staat de 30° en 60° breedtecirkel verwijderd van de evenaar bij de Merkatorafbeelding?

2)Bereken welke de drootte is van een breedtecirkel op 40° bij een normale azimuthale afbeelding van Lambert?

Bedankt

PS: weet iemand goede sites over cartografie?

pardon

Reinoutgoossens schreef:Kan iemand mij uit de nood helpen bij de volgende vraagjes:

1)Geg: r=2cm

Hoe ver staat de 30° en 60° breedtecirkel verwijderd van de evenaar bij de Merkatorafbeelding?

2)Bereken welke de drootte is van een breedtecirkel op 40° bij een normale azimuthale afbeelding van Lambert?

Bedankt

PS: weet iemand goede sites over cartografie?

De absolute bijbel voor kaartprojecties is dit boek:

Snyder, J. P. Map Projections--A Working Manual. U. S. Geological Survey Professional Paper 1395. Washington, DC: U. S. Government Printing Office, 1987

http://onlinepubs.er.usgs.gov/djvu/PP/PP_1395.pdf

http://mathworld.wolfram.com/CylindricalProjection.html

formule voor mercator:



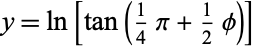http://en.wikipedia.org/wiki/Lambert_azimu...area_projection

formule voor poolcoordinaten:



De rest mag je zelf doen

Als de topichouder uitgaat van een bol van een straal van 2 cm,heb je een diameter van 4 cm en een bolomtrek=evenaars omtrek = meridiaansomtrek van pi * 4 cm=125,66371 mm.

De lengtegraden (NZ) hebben een verdeling van 2 * 180 graden (Oosterlengte en Westerlengte,beginnende in Greenwich met de 0-meridiaan) en de breedtegraden 2* van 0 (beginnende vanuit de evenaar) tot de polen = 90 graden.

Verder dus ook een beetje rekenen op basis van je gegeven bolstraal!