1 van 1
Norm lineaire operator
Geplaatst: wo 21 jan 2009, 17:08
door dirkwb
[attachment=3110:1.PNG]
Ik heb dit:
\( ||A||_2^2 \leq \frac{1}{2} \cdot ||f||_2^2 \)
dus
\( ||A|| \leq \sqrt{ \frac{1}{2} }\)
En hoe kies ik nu f
0 zodat
\(\frac{||Af_0||}{||f_0||} \)
maximaal is?
Re: Norm lineaire operator
Geplaatst: wo 21 jan 2009, 17:47
door PeterPan
\( ||A||_2^2 < \frac{1}{2} \cdot ||f||_2^2\)
(tenzij f=0 b.o.).
Dus
\(\frac{||Af_0||}{||f_0||}\)
heeft geen maximum.
Wel een
supremum.
Re: Norm lineaire operator
Geplaatst: wo 21 jan 2009, 18:22
door dirkwb
Wel een supremum.
Ok, hoe bepaal ik het supremum?
Re: Norm lineaire operator
Geplaatst: wo 21 jan 2009, 18:46
door PeterPan
Maak een rij functies
\(f_n\)
, waarvoor
\(\lim \frac{||Af_n||}{||f_n||} = ||A||\)
.
Merk op dat
\(\frac{x}{2x+1} \approx \frac12\)
voor grote waarde van
\(x\)
.
Dus zou je kunnen kiezen voor
\(f_n\)
een indicator met drager voorbij
\(x=n\)
.
Re: Norm lineaire operator
Geplaatst: wo 21 jan 2009, 19:41
door dirkwb
PeterPan schreef:Maak een rij functies
\(f_n\)
, waarvoor
\(\lim \frac{||Af_n||}{||f_n||} = ||A||\)
.
Merk op dat
\(\frac{x}{2x+1} \approx \frac12\)
voor grote waarde van
\(x\)
.
Dus zou je kunnen kiezen voor
\(f_n\)
een indicator met drager voorbij
\(x=n\)
.
Zoiets heb ik eerder in mijn dictaat gezien, maar ik snap niet waarom het iedere keer een indicatorfunctie is en ik snap ook niet hoe die rij eruit moet zien

Re: Norm lineaire operator
Geplaatst: wo 21 jan 2009, 21:36
door PeterPan
Neem
\(f_n(x) = 1_{[n,n+1)}(x)\ \mbox{d}x\)
.
Wat is dan
\(\int_0^{\infty}f^2_n(x)\ \mbox{d}x\)
en wat is
\( \int_0^{\infty}\frac{x^2}{(2x+1)^2} f^2_n(x)\ \mbox{d}x\)
en wat is dan
\(\lim \frac{||Af_n||}{||f_n||}\)
.
Waarom een indicatorfunctie? Wel, omdat je dan een
eindige simpele integraal hebt.
Re: Norm lineaire operator
Geplaatst: do 22 jan 2009, 08:19
door dirkwb
PeterPan schreef:Neem
\(f_n(x) = 1_{[n,n+1)}(x)\ \mbox{d}x\)
.
Wat is dan
\(\int_0^{\infty}f^2_n(x)\ \mbox{d}x\)
\( \int_n^{n+1}\ 1^2\ \mbox{d}x =1 \)
en wat is
\( \int_0^{\infty}\frac{x^2}{(2x+1)^2} f^2_n(x)\ \mbox{d}x\)
Bedoel je dit:
\( \int_n^{n+1} \left( \frac{x}{2x+1} \right) ^2\ \mbox{d}x\)
?
Waarom een indicatorfunctie? Wel, omdat je dan een eindige simpele integraal hebt.
Maar vaak neemt mijn docent bij de indicatorfunctie [n,n+1], maar niet altijd, daarom raak ik verward.
Re: Norm lineaire operator
Geplaatst: do 22 jan 2009, 18:02
door dirkwb
De opgave reuploaded:
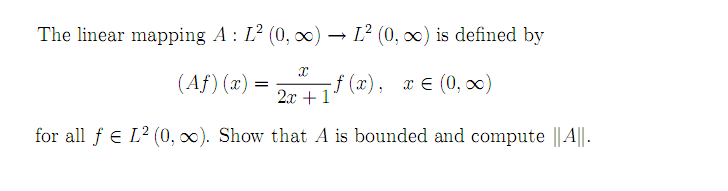
- 1 748 keer bekeken
Re: Norm lineaire operator
Geplaatst: vr 23 jan 2009, 20:06
door PeterPan
Bedoel je dit
\( \int_n^{n+1} \left( \frac{x}{2x+1} \right) ^2\ \mbox{d}x\)
?
Ja.
Je hoeft niet per se de indicatorfunctie
\(1_{[n,n+1]}\)
te nemen.
Je mag ook
\(1_{[\sqrt{n},\sqrt{n+1}]}\)
nemen.
Maar ik houd het liever zo eenvoudig mogelijk.