Uit een werkstukje van mij van enkele jaren terug:
Vind alle mogelijke rijen die voldoen aan
\((u_n)_{\nin\mathbb{N}}:u_{n+1}=u_n+u_{n-1}\)
. Wat heeft dit te maken met
\(\phi=\frac{1+\sqrt5}{2}\)
?
Beschouw
\(V={(u_n)_{\nin\mathbb{N}}|u_{n+1}=u_n+u_{n-1}}\)
. Het is eenvoudig
na te gaan dat
\(\mathbb{R},V,+\)
een vectorruimte is. Een eenvoudige
basis van
\(V\)
is
\(\beta={(0,1,1,2,3,5,\ldots),(1,1,2,3,5,8,\ldots)}\)
. Met
\(\beta\)
zelf zijn we niet bijster veel, maar we weten nu wel dat twee
lineair onafhankelijke rijen uit
\(V\)
steeds een basis voor
\(V\)
vormen. Stel nu
\(r=\frac{1+\sqrt5}{2}\)
en
\(s=\frac{1-\sqrt5}{2}\)
.
Omdat
\(r\neq s\)
geldt dat de rijen
\((a_n)_{\nin\mathbb{N}}=(1, r, r+1, \ldots)\)
\((b_n)_{\nin\mathbb{N}}=(1, s, s+1, \ldots)\)
een basis voor
\(V\)
vormen. Uit het voorgaande weten we echter dat
\(r^2=r+1\)
,
\(r^3=r^2+r\)
,
\(r^4=r^3+r^2\)
, enzovoort (analoog voor
\(s\)
).
Dus de meetkundige rijen
\((a_n)_{\nin\mathbb{N}}:a_n=r^n\)
en
\((b_n)_{\nin\mathbb{N}}:b_n=s^n\)
vormen een basis voor
\(V\)
. We
besluiten dus dat
\(\forall(u_n)_{\nin\mathbb{N}}\inV:\exists\lambda,\mu\in\mathbb{R}:\forall \nin\mathbb{N}:u_n=\lambdar^n+\mu s^n\)
Dit laat ons toe om op een gemakkelijke
manier een expliciet voorschrift te vinden voor een
\((u_n)_{\nin\mathbb{N}}\in V\)
. Kies bijvoorbeeld de rij van
Fibonacci. Omdat
\(f_0=f_1=1\)
geeft de kwantorenuitspraak aanleiding tot het stelsel
\(\left{ \begin{array}{\ll} \lambda+\mu=1\lambda r+\mu s=1\end{array} \right.\sim\left{ \begin{array}{\ll} \lambda=\frac{1-s}{r-s}=\frac{\sqrt5}{10}+\frac{1}{2}\mu=\frac{r-1}{r-s}=\frac{1}{2}-\frac{\sqrt5}{10}.\end{array} \right.\)
Dit strookt inderdaad met de formule van Binet.
Het kan zijn dat je hier en daar een indexje moet aanpassen, maar het idee is volgens mij juist.
N.D.
)
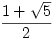en voor b, de andere uitkomst van de kwadratische vergelijking nemen? ( 
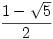dus)?
